萌新眼中的計算機與機器學習（一）圖文重製版

昨晚文章發佈之後大家在評論區提出了很多意見，其中最主要的大概就是缺少配圖，以及沒有機器學習相關的內容。所以我又重做了這一期圖文重製版，希望大家能繼續給我建議，每條評論我都有看。

另外前兩期應該確實不會涉及機器學習相關的乾貨......因爲其實我是想從圖靈開始講述“計算機”是如何從一個只會加減乘除的機器到現在擁有ChatGPT這樣的”智能“的。然後就是再次強調我只是一枚大二本科生，知識面和相關見解都非常有限而且粗淺，所以寫出來的東西價值不及大佬十一，大家可以把它們當作睡前讀物或者交流貼，有錯誤甚至謬論也很正常，希望大家能在評論區或者私信給我指正，謝謝大家！

圖靈與可計算理論

1.寫在算法之前

首先是要介紹圖靈的”哲學思想“——什麼樣的問題是可以用算法解決的？

”算法“一詞，在數據結構教材中有着詳細而恰當的定義，但對於我們理解計算機來說，只需要把握最核心的一點就夠了——算法就是按順序一步一步解決問題的方法。

在過去算法受到重視以前，如牛頓的時代，數理問題的解決主要依賴於天才們一閃而過的靈感與驚人的創造力。對於複雜的問題，他們總能以敏銳的洞察力和高超的技巧發現並揭示問題的核心，並將其轉化爲易於理解和處理的問題加以解決。比如下圖給出的歐拉關於巴塞爾問題的求解方法：

1975年，年僅28歲的歐拉得到了巴塞爾問題的正確解，解決了這個曾困擾牛頓和萊布尼茨等大神的難題

巴塞爾問題是指所有自然數平方的倒數之和的極限是多少的問題。在上面歐拉給出的解法中，最妙的地方之一就在於歐拉對正弦級數和根與係數關係的深刻把握。但問題也顯而易見，對大多數人來說，怎麼把它們和巴塞爾級數聯想到一起呢？

在牛頓到高斯的時代，上述天才”靈光乍現“的例子還數不勝數，這一過程固然富有觀賞性，但我們也不難想象缺乏這般天賦的大多數人對此只能望洋興嘆。

2.算法——機器的福音

然而算法的思想卻與上述解題過程截然相反——算法是設計好的步驟的集合，任何人（當然，機器也一樣）只要老老實實按照順序執行這些步驟，最終都能得到正確答案。比如下面這個判斷一個自然數n是否是素數的算法(這裏假定1是素數)：

步驟1.給定n，如果 n = 1，則返回 true，算法結束

步驟2.如果 n = 2 或 n = 3，則返回 true ，算法結束

步驟3.對於每個 i 從 2 到 n-1，依次執行以下步驟： 

                  如果 n 能被 i 整除，則返回 false ，算法結束

步驟4.步驟3中的n-1個數都不能整除n，返回 true，算法結束

在上述算法中，”返回”代表我們找到了問題的答案。返回“true"代表n是素數，返回”false"代表n不是素數，找到問題答案後，緊跟着的就是“算法結束”。

比如對於35，我們依次執行上述算法：

步驟1.給定35，如果35! = 1，繼續執行步驟2

步驟2. 35!=2且35!=3，繼續執行步驟3

步驟3.對於每個 i 從 2 到 n-1，依次執行以下步驟： 

                  初始時，i=2，35不能被2整除，i=2+1=3；

                  i=3,35不能被3整除，i=3+1=4;

                  i=4,35不能被4整除，i=4+1=5;

                  i=5,35能被5整除，返回false,算法結束

步驟4.步驟3已經得到問題答案，無步驟4

所以最終答案是"false"，35不是素數！我們可以驚喜的發現，上述算法只需要掌握三種基本運算即可進行，也即比較運算，+1運算，整除運算。而且只要你是嚴格按照以上步驟執行而沒有遺漏其中某步，最終一定能得到正確答案。雖然我們一眼就能看出來35能被5整除，所以35肯定不是素數，但這個算法的威力就在於，即使是對4294967297（2^32+1）這樣可怕的數字，我們只要按照上述步驟執行，最後總能找到正確答案——而這時候，想要通過眼睛觀察出4294967297的兩個質因數（641和6,700,417）而得到“4294967297不是素數”的結論，就不那麼容易了。

總之，算法思想隱含的就是這樣一個“福音”——不管“你”有多白癡，只要你會做加減乘除和比較大小之類等基本運算，你都可以按照給定的步驟一步步拆解並最終得到一個複雜問題的正確答案。這不僅對“你”來說是福音，對機器也同樣如此。

3.問題來了，什麼是“基本運算”？

上面說到算法實現了讓一個只會加減乘除等基本運算的“白癡”也能正確地解決複雜問題。那麼現在問題又來了，到底什麼是“基本運算”？微積分是基本運算嗎？矩陣的奇異值分解是基本運算嗎？事實上，我們發現這些複雜的數學計算大部分都可以用一系列加減乘除等更基本地運算來加以實現或近似——這沒關係，計算機本來就不可能處理一個真正的無理數，因爲存儲它需要無窮多個存儲單元，我們只能在精度允許的範圍內得到“正確答案”。而加減乘除等運算又可以進一步分解爲若干步的“與或非”等二進制運算（之所以要繼續分解，自然是因爲計算機只能處理二進制數）——沒錯，某種意義上這也是一種“算法”——如何用一串有序的二進制運算來實現整數的加減乘除，比較大小。

對計算機來說，什麼是最基本的運算？是剛纔提到的“與或非”嗎？不是的，其實“與門”“或門”“非門”都可以用最簡單的門——“與非門”實現（感興趣的可以學習《離散數學》中的聯結詞完備集）。而且除了這些邏輯和算術運算之外，我們還需要計算機做其他操作，比如存儲數據，讀取數據，等等，這些“基本操作”的定義隨着我們的需求的變化不一而足。下圖是一個簡單的模型機的指令集，它給出我們對計算機所理應能夠執行的“基本運算”（說操作/指令也許更合適）的較低期望：

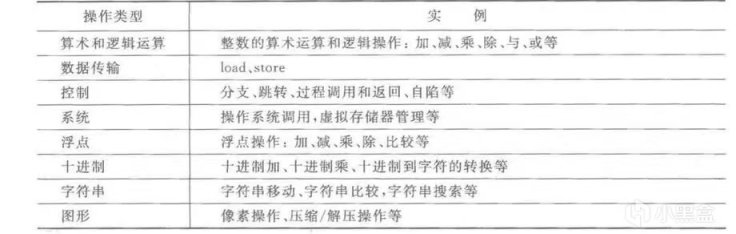
指令系統結構中操作的分類

對於“基本操作”的問題，尤其是我們很關心的指令集完備性問題，以及如何用二進制與或非運算實現整數的加減乘除的問題，在《計算機組成原理》這門課中還會有詳細的討論，在此就不再繼續展開了（應該是可以的吧......）

4.小結

至此我們討論了算法的底層思想和它是如何對計算機起作用的。但我們並不欲回答開篇的問題——“什麼樣的問題是可以用算法解決的”。這是一個相當困難而複雜的問題，還與千禧年7大難題之一的“NP猜想”有關，至少筆者還沒有能力觸及該問題的皮毛。不過可以肯定的是，一定有問題是不能用算法解決的，比如著名的“停機問題”。關於這方面的知識，有興趣的讀者可以自行學習《形式語言與自動機》，該問題相應的理論是開頭提到過的計算機科學的一大分支“可計算性理論”。

不過以上討論對我們來說已經夠用了，我們知道了什麼是算法，而且我們確實發現許許多多的問題都可以用算法解決——對我們來說，剩下的任務就是將算法國度的疆界不斷擴大，不斷創造/發現算法去解決各種各樣的問題。當然在此之前還有一個問題是留待下一篇帖子解決的——我們怎樣實現計算機自動地執行算法？（或者說，“計算器”與“計算機”的區別在哪裏？）

PS：人類歷史上最早的算法大約可以追溯到兩河流域的美索不達米亞文明，那時的美索不達米亞人已經發明瞭求根號2的算法，下面是某中學教材中對此算法的說明，讀者可自行探究其原理及正確性。

美索不達米亞人的開根號算法

另外樓主本人水平十分有限，再次感謝大家的閱讀，有不妥甚至錯誤的地方請大家在評論區指出或者私信我，我每條評論都有認真看！謝謝大家的鼓勵和建議！！！下一篇我打算將馮諾依曼和數字化——計算機如何像人類一樣處理各種（聽覺，視覺等的）信息，離講到正題機器學習恐怕還有點遠！但我是想從一切的最開始出發去體會計算機如何從賓夕法尼亞大學的那個笨重的龐然大物蛻變爲今天ChatGPT這樣的“人工智能”的大家對思路安排上有啥建議可以直接私信我。另外最近期末周恐怕沒多少時間寫帖子，下一篇不知道要鴿到什麼時候了

關於轉載：大家最好不要隨意轉載，因爲樓主水平實在太差了，寫的帖子很可能漏洞百出，別到了最後以訛傳訛就不好了。但歡迎大家針對帖子的內容隨意討論！