關於一道小學題的完整證明

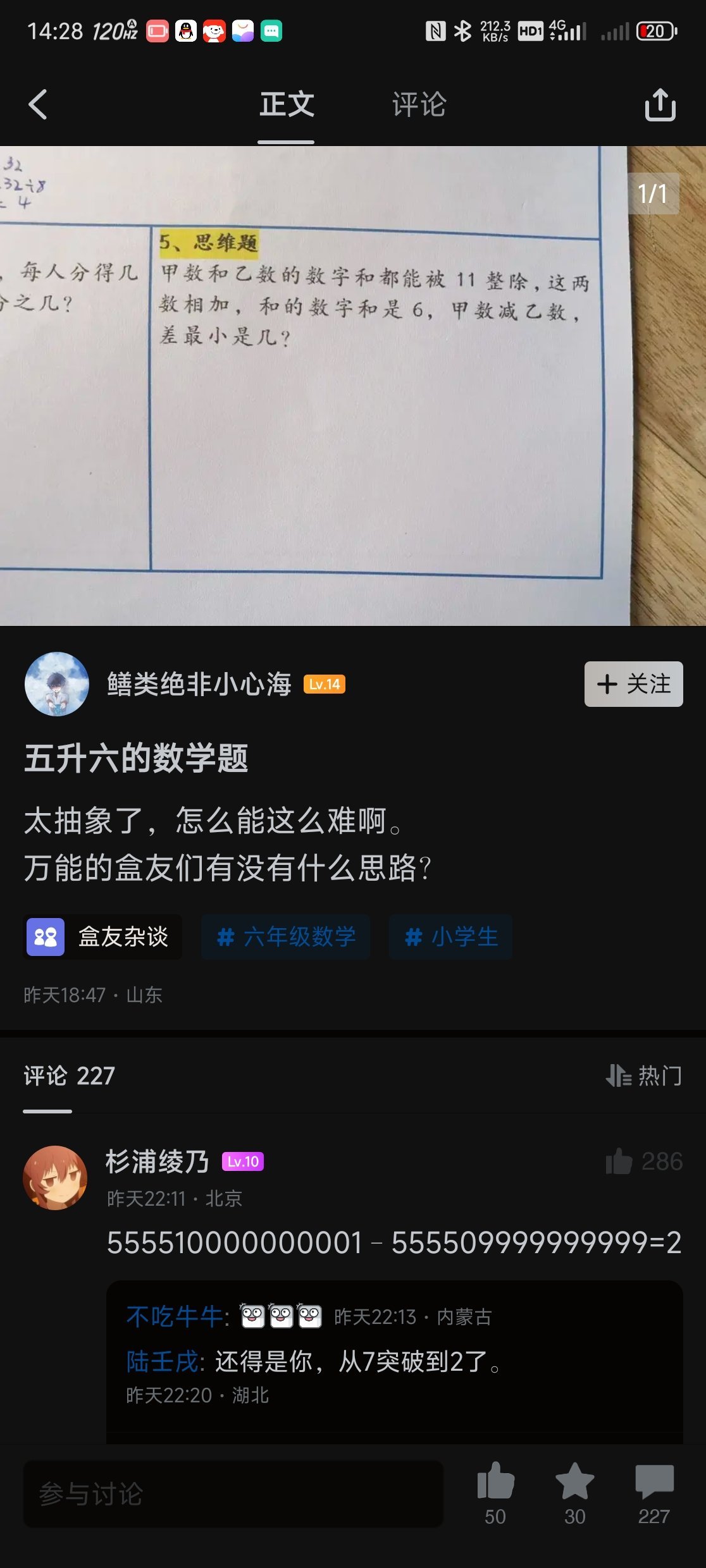
原貼：https://api.xiaoheihe.cn/v3/bbs/app/api/web/share?link_id=d4b670b7ed40 

今天刷到這個題，想構造一下，沒忍住就寫了一下構造過程證明，結果沒想到黑盒評論區太長的放不下，遂單開一貼寫一寫具體如何找到滿足這種要求的值。

考慮如何在64位整型暴力枚舉這種值，已經有人給出了1e16量級的數，而64位無符號整型的量級位1e20左右，如果僅僅暴力枚舉，普通家用CPU147k全核跑滿也得跑兩千多年，若寫cuda讓GPU來跑，普通家用GPU4090得跑六十多年，相對快一點，但依舊不現實。

記數x的數位和爲sum(x)，我們小學學過，一個數與其數位和模9同餘，即x≡sum(x)mod9，我們記小數爲x、差值爲d，則有2x+d≡6mod9，解得x≡5(6-d)mod9，我們其實已經知道d最小值爲2，則x≡2mod9，這樣枚舉起來就可以九個一枚舉，搜索空間一下就縮小了不少，4090只需要跑幾年就能跑完了。

注意到，如果x+d只有個位數與x不同，顯然不可能滿足兩者的數位和均爲11的倍數的情況（因爲此時兩者的數位和差值也爲d），因此加d後必然進位，以這裏的2爲例，能夠進位的小數的個位數只有8與9，對應大數的個位數爲0與1，其中小數個位數爲8的情況顯然不成立，因爲此時個位數的值就已經爲8，顯然不可能滿足兩者和的數位和爲6的條件，因此小數的個位數必然爲9，即x≡9mod10，再結合前面的x≡2mod9，由中國剩餘定理可以得到x≡29mod90，這樣我們的搜索空間又縮小了十倍，單卡4090僅僅只需要跑幾個月就能跑完！

接着我們來討論十位的情況，前面我們已經知道x+d會導致十位加1，同時x的個位數爲9、x+d的個位數爲1，我們記x的十位數爲a，若十位加這個1之後不會出現進位，即a+1<10，則兩者的數位和的差則爲(a+9)-(a+1+1)=7，數位和差7，不可能數位和均爲11的倍數，因此十位也必然進位，a只能爲9，即x的後兩位只能爲99，x+2爲01，即x≡99mod100，再次可以縮小十倍範圍。

同樣地，我們可以討論百位是否進位，x的百位記爲a，若不進位，則數位差爲(a+9+9)-(a+1+0+1)=16，具有這樣差值的二者顯然也不會均爲11的倍數，因此x的百位依舊爲9，即x≡999mod1000，再次縮小了十倍範圍。

更一般地，我們可以討論加上這個2之後從個位起有k位都會進位，記第k+1位爲a，那麼小數的低k位均爲9、大數的低k位由k-1個0與1個1組成，兩者的數位差則爲(a+9k)-(a+1+1)=9k-2，要使兩者的數位和均爲11的倍數，因此有9k-2爲11的倍數，即9k-2≡0mod11，求解可得k≡10mod11，即x的末尾的9的個數可能爲10個、21個、32個……如果僅僅只是想在64位整型中尋找答案，那麼就已經縮小了相當的數量級，即便是CPU跑，用時也已經從兩千多年縮減到了幾秒鐘，到這一步就已經可以考慮暴力求解了。

但是都到這一步了，僅僅暴力枚舉顯然已經無法滿足我們的慾望，實際我們可以進一步探討。前面我們已經發現x的末k位爲9，其中k≡10mod11，因此x可以表示爲H*10^k-1，x+2則爲H*10^k+1，兩者的數位和爲11的倍數，即爲：

sum(H)+1≡0mod11，sum(H)≡10mod11，又由H最初始的定義（H-1加一後只改變個位）我們可以得到，sum(H-1)=sum(H)-1，因此sum(H-1)+1≡10mod11，得到sum(H-1)≡9mod11，即x的高位的數位和與9模11同餘。

另外，由於兩數之和的數位和爲6，兩數又分別爲H*10^k-1與H*10^k+1，因此sum(2H)=6，這意味着2H的每位數必然小於等於6，這裏我們記滿足sum(2N)=n的數N的數位組成集合爲S(n)，我們現在來討論S(6)，2H只能由0-6這七個數組成，對應H的位數爲0、1、2、3、5、6、7、8，其中當H的某位數爲8時，該位對sum(2H)的貢獻爲1+6=7，已經超過了6，因此8排除；當H的某位數爲7時，該位對sum(2H)的貢獻爲1+4=5，其他位的貢獻只能爲1，因此其他非位只能爲5，因此sum(H)=5+7=12，與前面我們推出的sum(H)≡10mod11相悖，因此7也排除；類似地，當H的某位爲3時，該位直接爲sum(2H)貢獻6，因此沒有其他非零位，此時sum(H)=3，排除；當某位爲2時，其他位的貢獻爲2，H的其他位只能爲0、1、5，準確說只能是一個1或者兩個5，對應的sum(H)分別爲3和12，因此2排除；當H的某位爲6時，該位貢獻了3，其他位貢獻3，因此H的其他位只可能爲0、1、5、6，其中若其他某位爲6，就不會有其他非零位，此時的sum(H)爲12，此處排除，其他位出現1的話就需要再補一個5，此時的sum(H)爲12，排除，其他位此時只可能爲5，若出現5就只能爲3個5，此時sum(H)爲21，暫時合法；若H某位爲1，其他位的貢獻則爲4，其他位只能爲0、1、2、5、6、7，類似的討論可以排除7、6、2、1，若爲5只能爲四個5；剩下只剩全5的組合，即六個5，此時sum(H)爲30，也可以排除。綜上所述，H（注意這個H是x+2的高位而非x的高位）只可能由一個1與四個5、或一個6與三個5構成，中間可由若干零填充，但由H的初始定義，H的末尾不能爲0。

更一般地，我們可以發現，sum(2N)=2sum(N)-9c，其中c爲2*N時的進位次數，因此2sum(H)-9c=6，sum(H)=3+9c/2（這個/表示普通除法），顯然由於sum(H)爲整數，c應當爲偶數，令c=2t，則sum(H)=3+9t，又sum(H)≡10mod11，故9t+3≡10mod11，t≡2mod11；記t=2+11m，c=4+22m，sum(H)=21+99m，當m=0時，c=4、sum(H)=21，有四個會產生進位（即大於4）的數、若干個數總和爲21，我們發現5*4=20，因此只可能爲四個5與一個1或者三個5與一個6的組合，與前面我們的結論吻合；而對於m大於0的情況，相當於sum(H)平均每新增9，就要增添兩個進位的數字，但這兩個數之和至少爲10，因此m只能爲0，同樣與前面我們的結論相符。

至此我們就完全掌握了這類數（數位和均爲11的倍數、和的數位和爲6、差值爲2）的構造規律，即H*10^k+1與H*10^k-1，其中k≡10mod11、H由末尾不爲0的由三個5一個六或四個5一個1以及若干零組成，比如顯然可以寫出滿足要求最小的數字爲55560000000001與55559999999999。