Sigmoid成了hy的 "測謊儀"：小南梁身份大揭祕！

(文章打趣內容純屬娛樂，請勿當真，要是侵犯到hy的眼睛，非常抱歉)

近期鼠鼠我發現一招，辨別hy是否爲小南梁的好方法——Sigmoid函數，只要將hy的等級傳入其中，就可以得到hy是否爲小南梁的結果！

Sigmoid在這裏並非西格瑪，而是一個函數。

而我們要利用它實現我們想要辨別小南梁的目的，需要將Sigmoid函數之力注入機器學習之中。下面是Sigmoid的本體，和相應的代價函數(交叉熵)，梯度公式

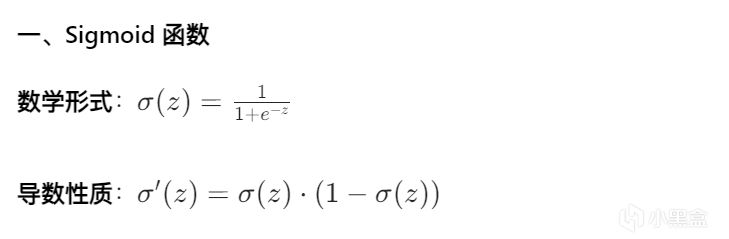
本體

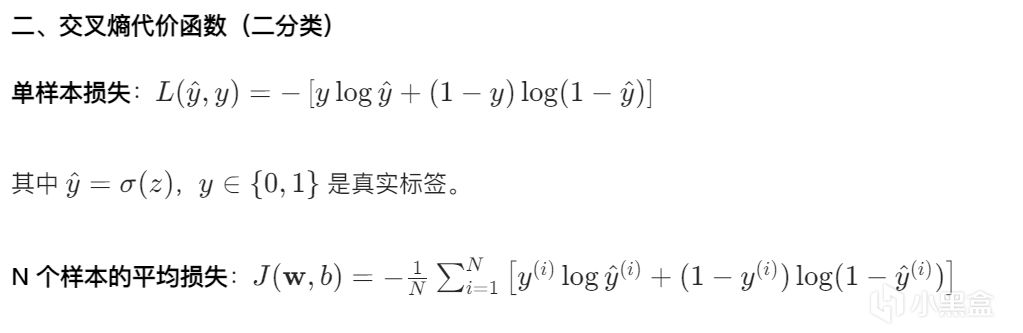
交叉熵代價函數

梯度公式

代碼如下

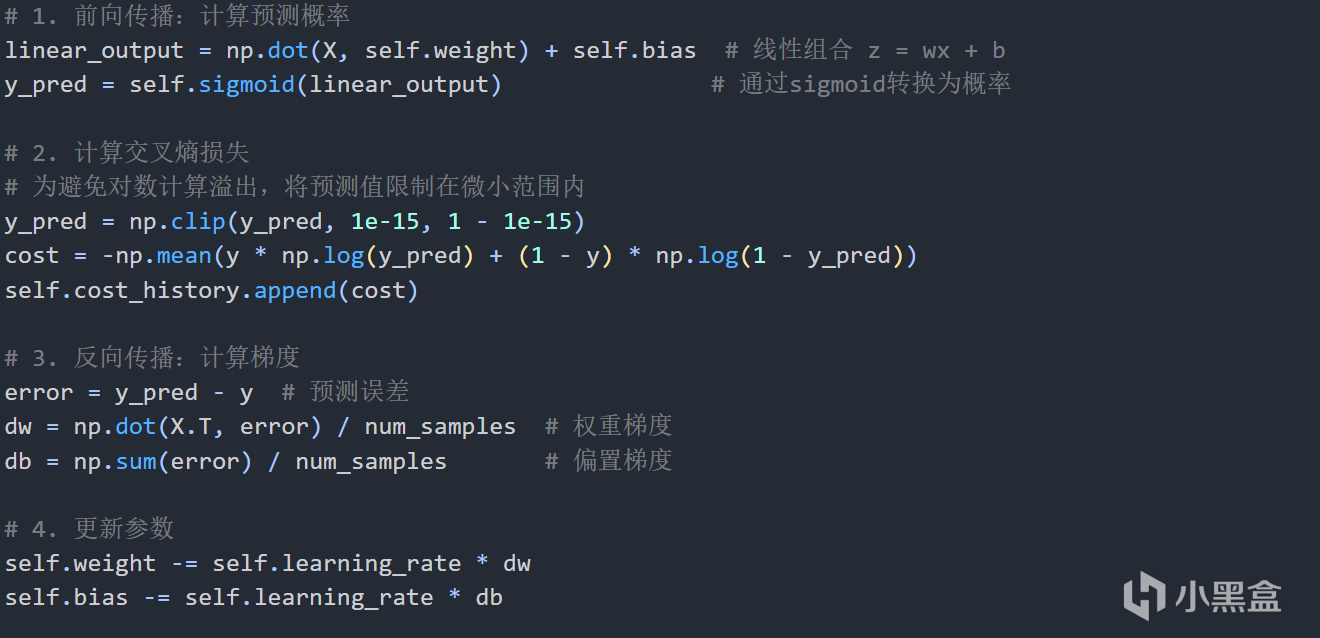
關於Sigmoid函數爲什麼使用交叉熵代價函數

對於二分類問題，標籤y∈{0,1}，我們希望模型輸出的預測概率y^=σ(z)接近真實標籤。

問題：當使用 Sigmoid 函數時，MSE 會導致代價函數非凸，存在多個局部極小值，梯度下降容易陷入局部最優。

正確選擇：交叉熵損失（Cross-Entropy Loss）

優勢：與 Sigmoid 函數配合時，能形成凸函數，保證梯度下降找到全局最優解。

若使用 MSE在y^接近 0 或 1 時會變得非常小，導致梯度消失，學習速度極慢。

而交叉熵避免了這個問題，無論預測值好壞，梯度都能保持合理大小，確保學習效率。

交叉熵代價函數來源參考最大似然估計相關內容

首先先拿我潛伏小黑盒多年的數據呈上(bushi)

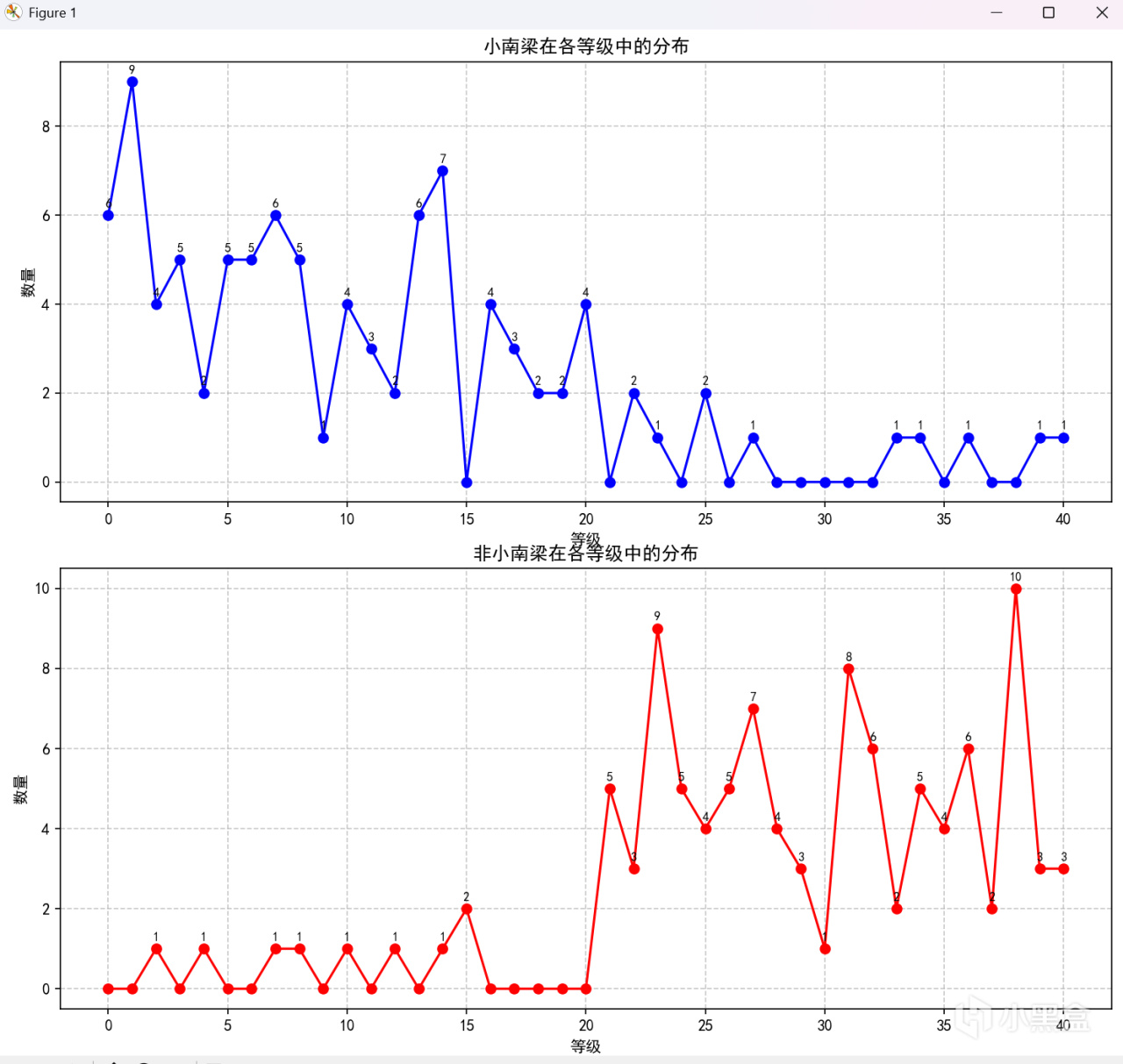
分佈折線圖

現在調整學習率，調整迭代次數，我希望讓我的模型更加準確一點，損失函數值儘量小，再參考等級大致在0~40，我選擇學習率爲0.001，迭代次數100000次

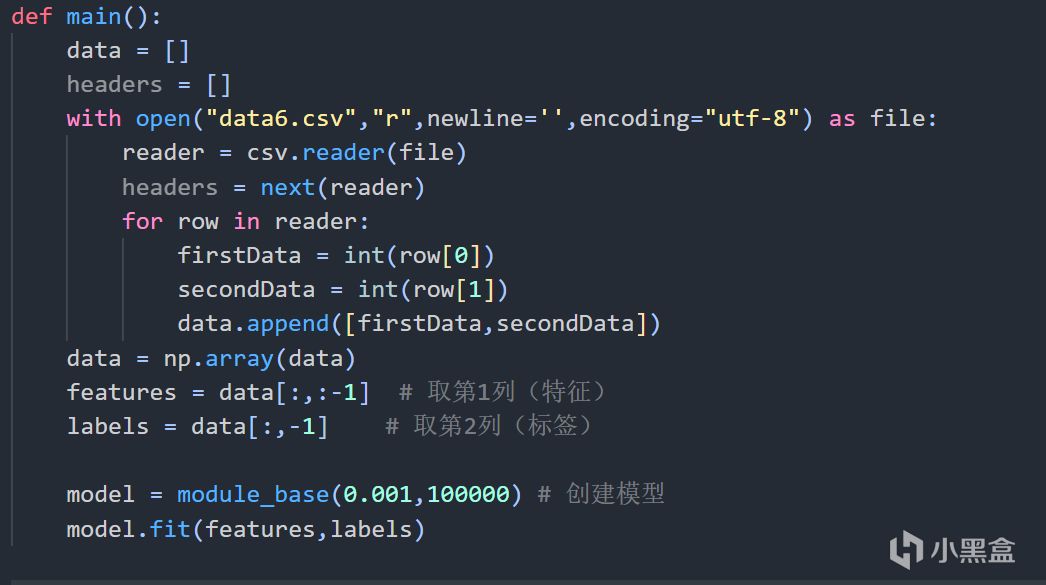
代碼

代價函數值輸出結果

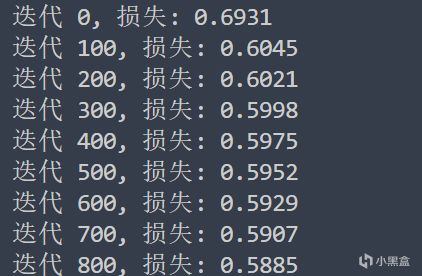
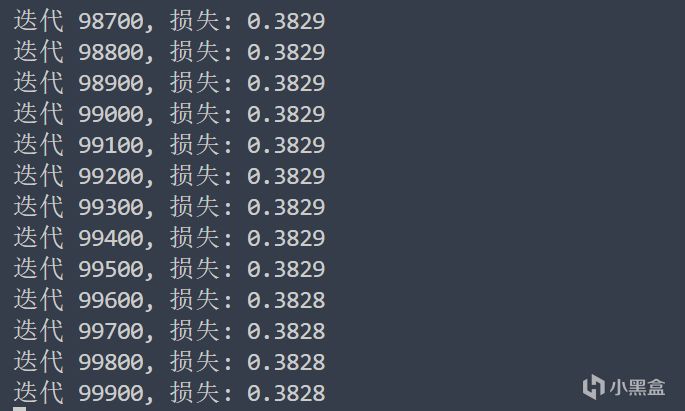
後面我也試了很多參數，最小值差不多都在這個範圍左右，可以說模型應該很準確了吧

直接測試一下吧，先來個20級別老登測試一下

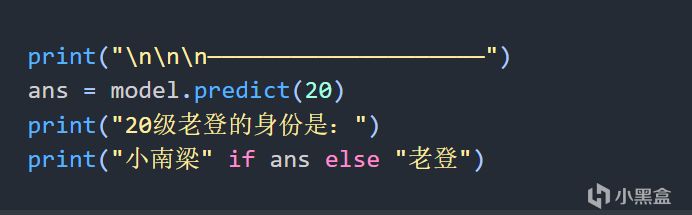
代碼

輸出結果

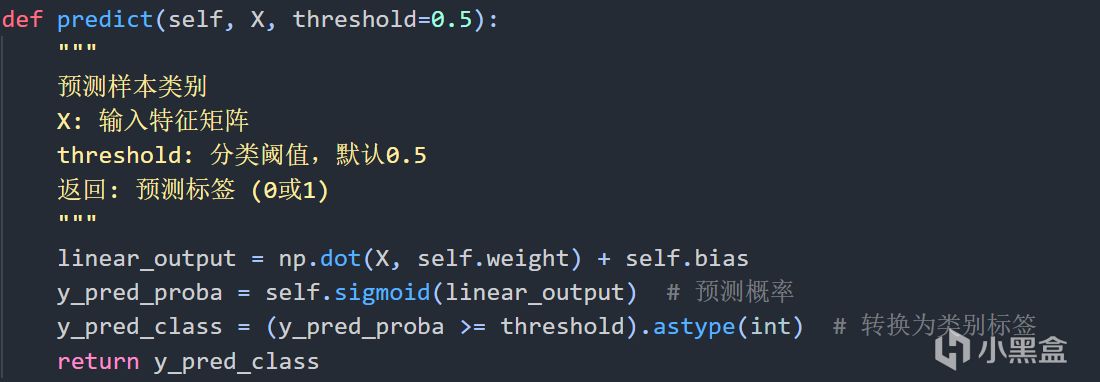
測試函數

我累個，居然不是小南梁，我看看我的等級——10看看

代碼

輸出結果

，好好好，忘了按照結果輸出了

下次要在捏造數據的時候把閾值放到九級

下面是分割線

————————————

分類算法有非常多，sigmoid屬於分類算法的一種。

sigmoid算法做的很厲害的一件事就是將輸出y值控制在了0-1，但是仍然可以將sigmoid函數自變量看成線性或者非線性的其他函數，這讓sigmoid的泛用性也很強，不僅僅是處理一個特徵，多個也是可以的。