最新研究！爲什麼時間旅行可能又不可能？

在理論物理學中，封閉類時曲線（Closed Timelike Curve, CTC）被認爲是時間旅行的理論載體。這種特殊的時空結構允許物體沿着時空路徑運動後返回自身的過去。

經典祖父悖論（圖片來源網絡）

然而，近期範德比爾特大學的L Gavassino在《經典與量子引力》期刊發表的最新研究表明，這種旅行有着根本性限制：

任何沿CTC運動的宏觀系統（包括載人飛船），其內部狀態將在旅程結束時被強制重置，旅途中形成的所有記憶將被徹底擦除。

一、熱力學時間箭頭的困境

熱力學第二定律指出，孤立系統的熵（無序度）永不減少，這定義了時間箭頭的方向——"未來"即熵增方向。但在CTC的閉環結構上，熵的行爲面臨根本矛盾：

熵的連續性要求：熵是描述系統狀態的連續函數
閉環上的極值點：在CTC的緊緻集上，熵必存在最小值點x₀和最大值點x_f

由此推得關鍵結論：

從x₀（低熵）到xf（高熵），熵必須增加——這定義了"未來"方向
然而CTC是閉環結構，從xf返回x₀的路徑上，熵必須從高值減少回低值
因此在xf附近，熱力學時間箭頭髮生反轉

沿 CTC 的時間熵箭頭（灰色箭頭）。箭頭的正意義跟隨熵的增加，這些是最小和最大熵事件，它們標誌着同一艘宇宙飛船的兩個平行歷史（藍色和綠色）的開始和結束。

論文Figure 1：展示熵箭頭（灰色箭頭）沿CTC反轉。藍色和綠色路徑代表飛船的"兩條平行歷史"，均始於熵最小點x₀，終於熵最大點x_f。

二、研究核心思路

研究核心在於用量子統計力學解釋上述熱力學圖景的必然性。考慮軸對稱時空（如哥德爾宇宙）中，由角動量算符J生成的旋轉對稱性軌道。核心約束源於時空幾何的週期性：

繞對稱軸完整旋轉一週（角度變化2π）後，系統必須回到物理等價狀態。對應量子力學的基本定理（Wigner定理）：

ei2πJ = const = eiα

推導的核心步驟：

1.飛船的時間生成元：沿CTC飛行的飛船，其時間演化由角方向φ的平移生成

2.飛船的哈密頓量：驅動飛船內部演化的哈密頓量算符H與角動量算符J直接相關：

H=−2πJ T +const

其中𝒯是飛船完成CTC環路的固有時間。

3.物理狀態重置：將H表達式代入Wigner定理得核心方程：

e^−iHT =1

無論飛船內部系統（粒子、儀器、乘客）的初始狀態如何，在經歷固有時𝒯後，它必須精確回到初始量子態（僅允許全局相位變化）。歷史自動保持一致，無需額外假設。

三、由此引發的物理後果

1.能級的強制量子化

方程要求哈密頓量H的本徵值E必須滿足：

E= 2πn T , n ∈Z

對應論文公式(10)：能級離散化條件

這意味着飛船內部所有系統的能級間隔被強制爲2π/𝒯的整數倍，只有能級精確匹配此條件，系統才能在時間𝒯後完全迴歸初始態。

正如同鐘擺擺動頻率需是 1/𝒯整數倍才能在𝒯時間後回到起點。

圖片來源網絡

而這種能級間隔的尺度，會因旅程時間變化而不同：

1年旅程(𝒯≈3.16×10⁷秒)對應最小能級間隔小到僅爲~10⁻²²eV；只有當旅程時間短到~10⁻¹⁵ 秒 (飛秒量級) 時，間隔才達到1eV（原子能級尺度）。

2.熵增箭頭記憶擦除

假設飛船在x₀（熵最小點）處於高度有序的非平衡態，如不穩定粒子或帶有特定記憶的觀察者。

在從 x₀到 x_f 的旅途中，系統遵循常規規律，熵增演化趨向平衡態，不穩定粒子衰變，觀察者形成新記憶，在 x_f 附近達到或接近最大熵的平衡態。

然而，由於 e^{-iH𝒯} = I 的強制要求，結合 Poincaré 迴歸定理，在閉合類時曲線（CTC）上，能級量子化使得系統無論多複雜，都會在旅程結束時刻𝒯精確迴歸初始狀態，引發熵減。

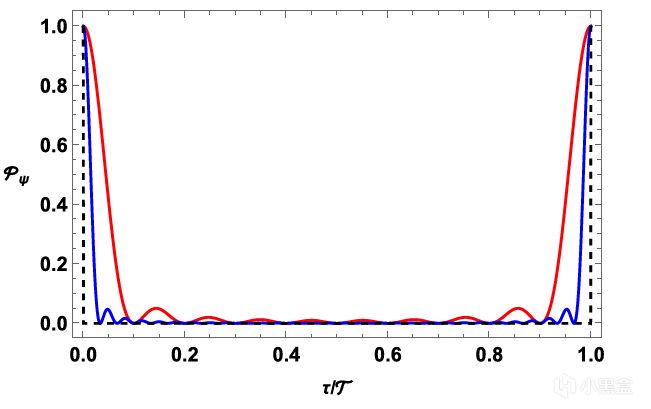
不穩定粒子在閉合類時曲線（CTC）上運動時的瞬時衰變及隨後的複合，其中 Z = 10（紅色），Z = 30（藍色），以及 Z → +∞（虛線）

論文Figure 2：不穩定粒子在CTC上的演化。粒子在τ≈0時衰變（熵增），在τ≈𝒯時重組（熵減）。

從 x_f 返回 x₀時，系統通過巨大的量子漲落被強制拉回初始低熵態，逆轉熵增過程。

而記憶作爲系統狀態對過去事件的編碼，在系統狀態迴歸到旅程起點 x₀時，旅途中形成的記憶會被徹底抹去，就像一個粒子在旅程中先衰變熵增，臨近結束時又通過量子漲落重組回初始狀態一樣，乘客最終只會記得出發前的事情，對閉環旅程毫無印象 。

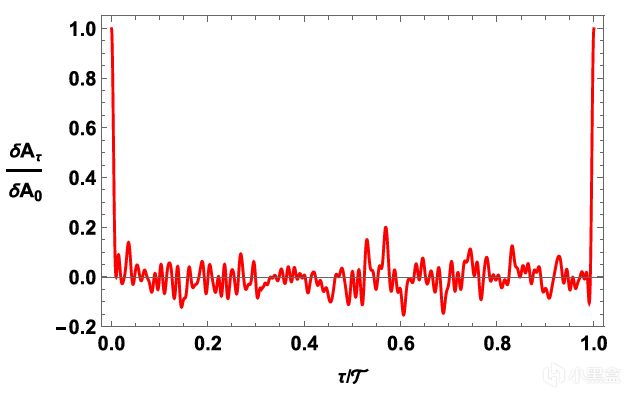
一個滿足本徵態熱化假設並沿閉合類時曲線（CTC）演化的熱力學系統中，一般量 A 的動力學演化。

論文Figure 3：宏觀系統在CTC上的演化。系統從非平衡態(τ=0)弛豫至平衡態，並在τ≈𝒯時迴歸初始態。

四、省流時間

基於以上機制，那些經典的時間旅行悖論被釜底抽薪般地化解了：

1、祖父悖論？不存在。歷史自動保持一致。你在旅程中做的任何事（比如試圖阻止祖父結婚），其影響都會被隨後的熵減過程“撤銷”，並在旅程結束時被徹底重置。你無法改變到達 x₀ 時的“過去”。

2、遇見年輕的自己？幾乎不可能。

方案一（單Bob）：飛船裏只有一個年輕的Bob。當他到達旅程終點 𝒯 時，方程e^−iH𝒯∣Young Bob⟩=∣Young Bob⟩
將強制他變回年輕的自己。年老的Bob要麼在途中死去，要麼在熵減過程中“返老還童”回年輕Bob。無論如何，兩個Bob無法共存。

方案二（雙Bob）：假設在 x₀ 點，通過巨大的量子漲落，憑空產生了一個年輕Bob和一個自稱來自未來的年老Bob。年老Bob的記憶（關於“未來”）很可能是虛假的，是低熵態 x₀ 隨機漲落的一部分。年輕Bob沒有任何理由相信這個年老“克隆人”真的是未來的自己，因爲圍繞 x₀，宏觀因果關係已失效。年老Bob的存在本身就是一個沒有（宏觀）原因的低熵事件。

3、留下記錄？ 不可能。任何在旅途中形成的記錄（筆記本、錄像、大腦記憶）都會在熵減階段被抹去，並在 𝒯 時刻重置回初始狀態。

因此，我們可以認爲，時間旅行者最深的困境，或許是無法證明自己曾進行過時間旅行。