來了來了!!書接上回,hym大概知道了構建模型的一個基本流程,現如今很多模型都是用的這樣的模式。但是還是很容易感受到,我們構建的模型,好像離實際的應用還遠的很,這是爲什麼呢?模型的構建流程如下
模型構建流程一般爲:明確目標與數據收集→數據預處理(清洗、特徵工程等)→選擇算法與模型架構→模型訓練→評估與調優→驗證與部署。
而我們上個模型在構建的時候,忽略了非常多的處理過程,但是不用擔心,我們將在後面的學習中慢慢補充這些內容。
首先,我們先關注數據的預處理。這裏我們引入一個概念,叫做
特徵縮放
特徵縮放(Feature Scaling)是數據預處理的關鍵步驟,指通過數學變換將不同特徵的取值範圍調整到同一數量級,消除特徵間尺度差異對模型的影響,確保算法性能不受特徵絕對值大小或量綱干擾。
核心作用:
避免數值大的特徵主導模型(如梯度下降優化時梯度方向偏差);
提升基於距離計算的算法(如 KNN、SVM)準確性;
加速模型訓練收斂速度(如神經網絡、線性迴歸)。
單單講概念是枯燥的,我來舉個例子給大家看看
假設現在我們要買房子,想要收集關於房子的信息,假設房子的買點在與房子的大小,房子臥室的數量,我們這裏假設臥室數量範圍浮動在(1~10),房子大小範圍浮動在(1~1000),房子價格根據這些來決定。現在網上有很多的諸如此類的數據,我們藉助python爬取了出來做了一個數據集,然後我們利用之前看過的構建模型的方法,多線性迴歸進行擬合(這裏我們假設線性相關),然後我們按部就班,生成對應的J函數關於向量W與b的等高線值圖像,如下圖1所示
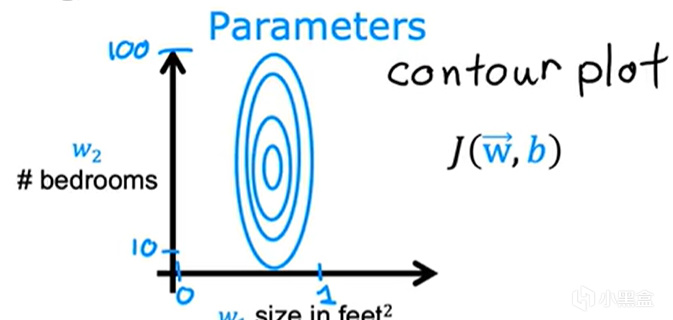
圖1
關於圖1
1.等高線圖的數學含義
J(W, b):表示代價函數(如均方誤差 MSE),是關於權重 W 和偏置 b 的二元函數。
等高線:圖中每條曲線代表J (W, b) 值相等的點的軌跡,類似地圖中的等高線(海拔相同的點連接成線)。
2. 等高線圖的關鍵構成
(1) 座標軸
橫軸:通常表示權重參數 W(或 W₁、W₂等多維權重中的某一維)。
縱軸:通常表示偏置參數 b。
(2) 等高線形狀
圓形 / 近似圓形:當 W 和 b 的尺度相近時,等高線呈圓形,梯度方向直指最小值點,優化路徑更高效。
橢圓形 / 狹長形:當 W 和 b 的尺度差異大時,等高線被拉長,梯度方向傾斜,導致優化路徑曲折(需多次迭代才能收斂)。
(3) 顏色 / 線條密度
顏色深淺:表示 J (W, b) 的值大小(如深色表示低代價,淺色表示高代價)。圖1沒表示清除,不用在意,一般是有顏色標記的,這裏方便直接截取的視頻中的圖。
線條密度:越密集的區域表示代價函數變化越快(梯度大)。
(4) 全局最小值點
等高線圖的中心(最內層閉合曲線)對應 J (W, b) 的最小值點,即最優參數組合 (W*, b*)。
可以看到圖1狹長,在進行對應的梯度下降時,會出現很大的問題。
在偏導求值時,由於學習率相同,數據大小變化更快的一端偏導更大,下降速度遠遠大於小的一方,而讓數據大的特徵值更容易影響模型,而小的特徵值對模型的影響很小。這樣會導致學習率在放入的時候,很難找到合適的值,例如房子大小在0~1000,假設又有一個特徵值在0~10000,諸如此類,那我們不得不根據數據變化最大的特徵值進行調整學習率,防止學習率過大而使得發生梯度爆炸(Gradient Explosion)
梯度爆炸
參數劇烈震盪:梯度方向頻繁反轉,導致參數在最優解附近大幅跳躍,無法收斂。
損失函數發散:迭代過程中損失值持續上升或劇烈波動,模型性能急劇下降。
數值溢出:極端情況下,梯度值超過計算機浮點數表示範圍,導致 NaN(Not a Number)錯誤。
原因:
學習率過大時,參數更新步長超過最優解的 “鄰域”,每次迭代都會跳過更優解,形成惡性循環。
而同時小數值特徵值對模型的影響也變得越來越小,使得模型擬合的速度大大下降。
這顯然不是我們想要見到的結果,那我們怎麼解決呢?
那我們就需要用到今天的重點了——特徵縮放
我們通俗的稱呼爲歸一化操作
聽這個名稱我們就可以知道,就是我們數學學習的將大的數值數據變成一個小的數據而選擇保持原數據之間的一些關係,例如數據之間的比例
而恰恰我們在研究梯度下降時,只是需要數據之間變化的速率關係,可以說是類似比例的層面,而不是簡單的數值大小關係。
恭喜!你已經找到了一個解決方法,現在我們需要來找幾個解決方案來實操了。
這裏我列出幾個方法,hym可以大概看看:
最大值歸一化:數據無負數,需縮放到 [0, 1],保留分佈,對異常值敏感
均值歸一化:數據有正負值,需中心化且縮放到 [-1, 1],保留分佈,對異常值敏感
Z-score 標準化:數據近似正態分佈,需保留分佈形狀,保留分佈,對異常值敏感
Min-Max 縮放:稀疏數據、已知邊界數據,需嚴格縮放到 [0, 1],不保留分佈,對異常值敏感
L1/L2 歸一化:向量相似度計算(如文本分類),需消除向量長度影響,不保留分佈,對異常值敏感
Robust 縮放:數據包含異常值,需消除向量長度影響,保留分佈,不對異常值敏感
在瞭解這些方法後,我們得知道歸一化是用在哪些數據上的,首先前面討論的是特徵向量數據,那對於標籤值y要不要呢?首先,可以肯定的是歸一化最多用於具有連續值的y,然後再分析具體情況如下
ai->總結
線性迴歸、嶺迴歸、Lasso:若特徵已歸一化,爲保持尺度一致性,可對 y 歸一化(但非必須,因模型會自動學習截距項)。
神經網絡、支持向量機(SVM)迴歸:若輸入特徵歸一化,輸出 y 歸一化可能加速訓練收斂。
終於是到了代碼部分,使用的庫和之前一樣
爲了更加好展示數據數值大小在歸一化和未歸一化下的差距,直接對房子大小進行史詩級升級,來到1~50000平方米!有點大,hym忍受一下(bushi)。
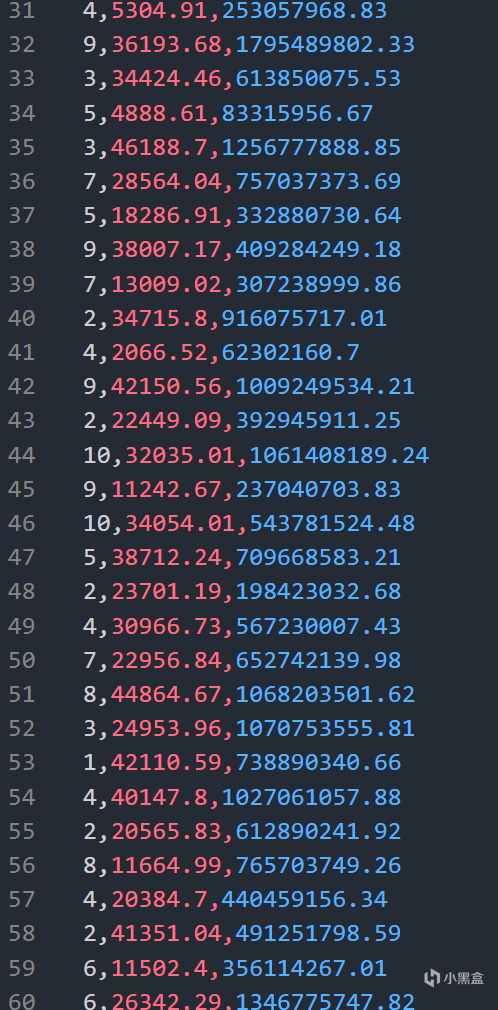
數據data3.csv
這是數據捏,房子還是蠻大的,房價。。。算了。。。
模型的一些基礎操作就不貼圖了,先演示一下用牢模型結合不同的學習率看看效果展示一下效果
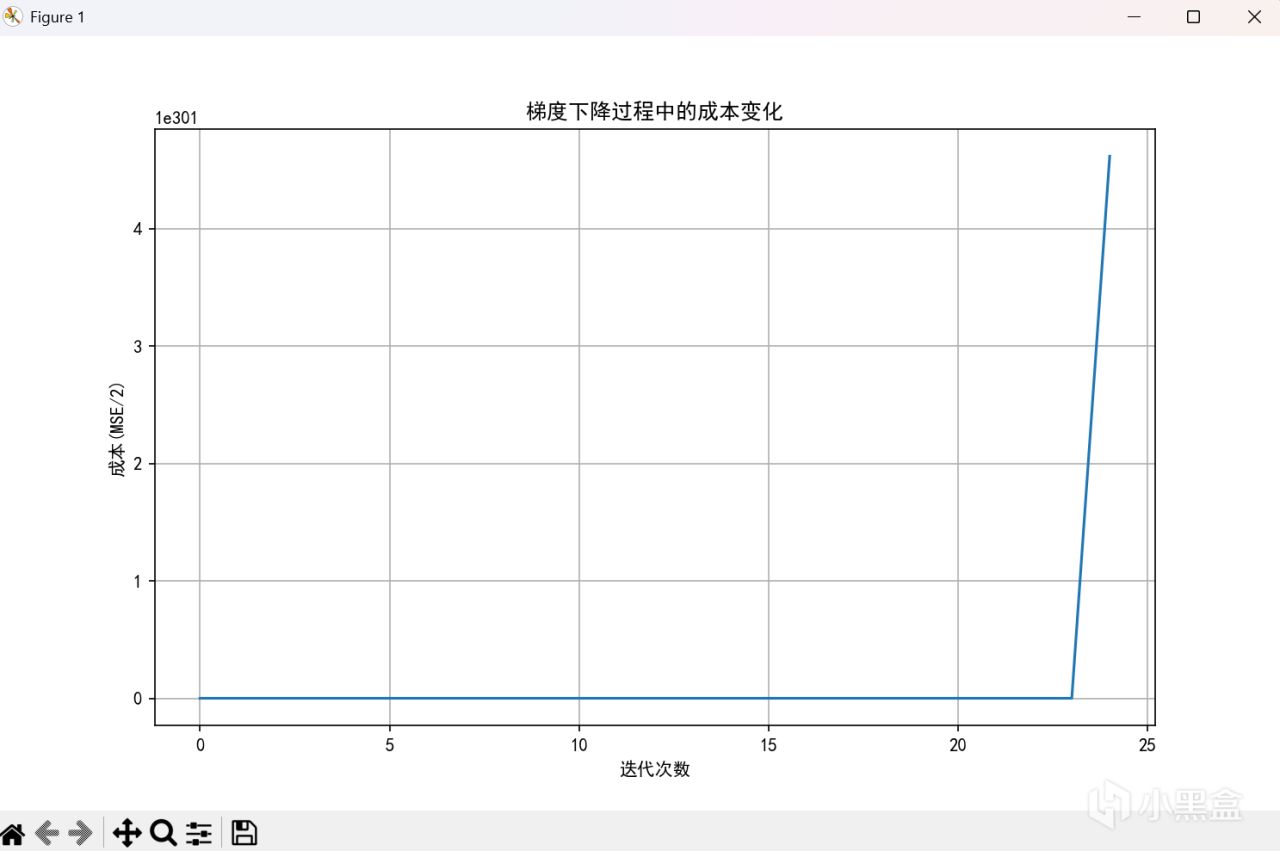
alpha = 0.001
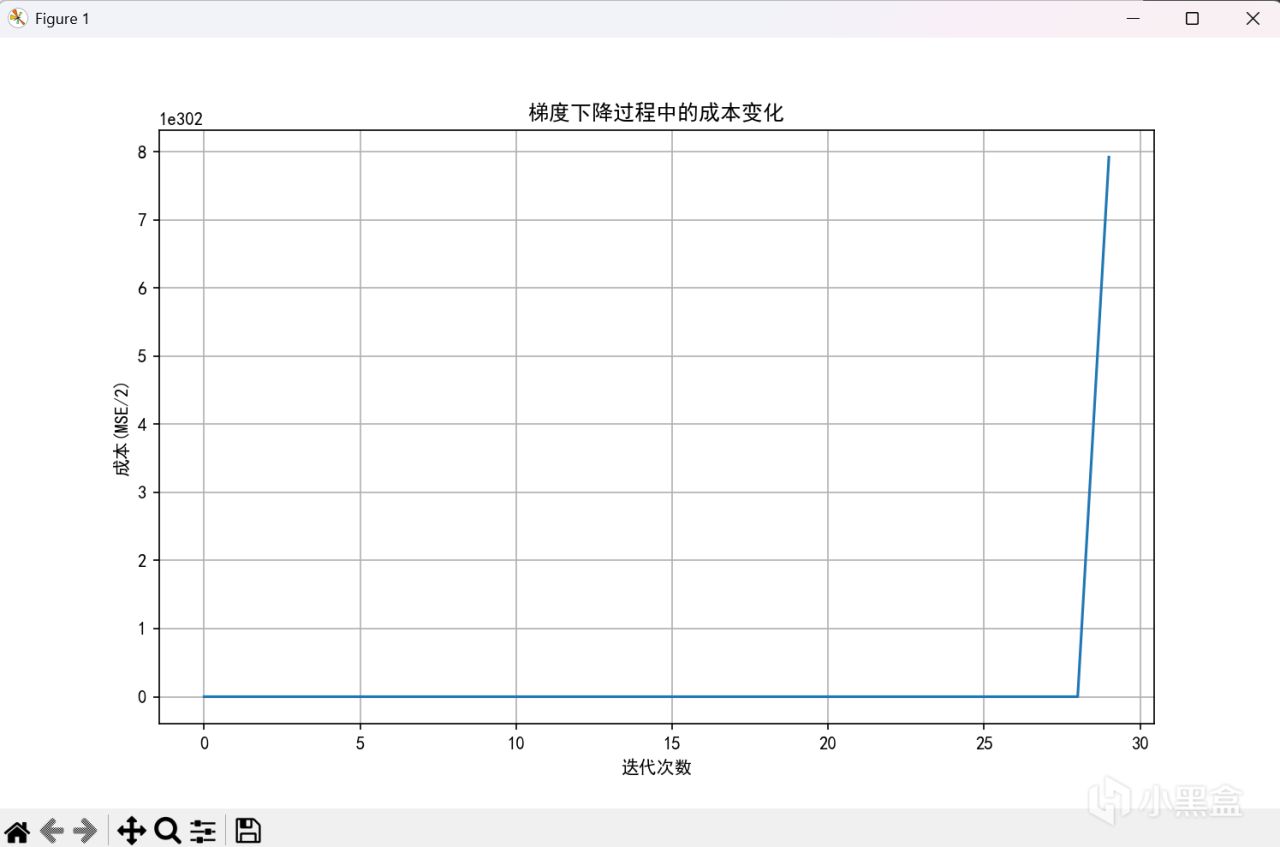
alpha = 0.0001
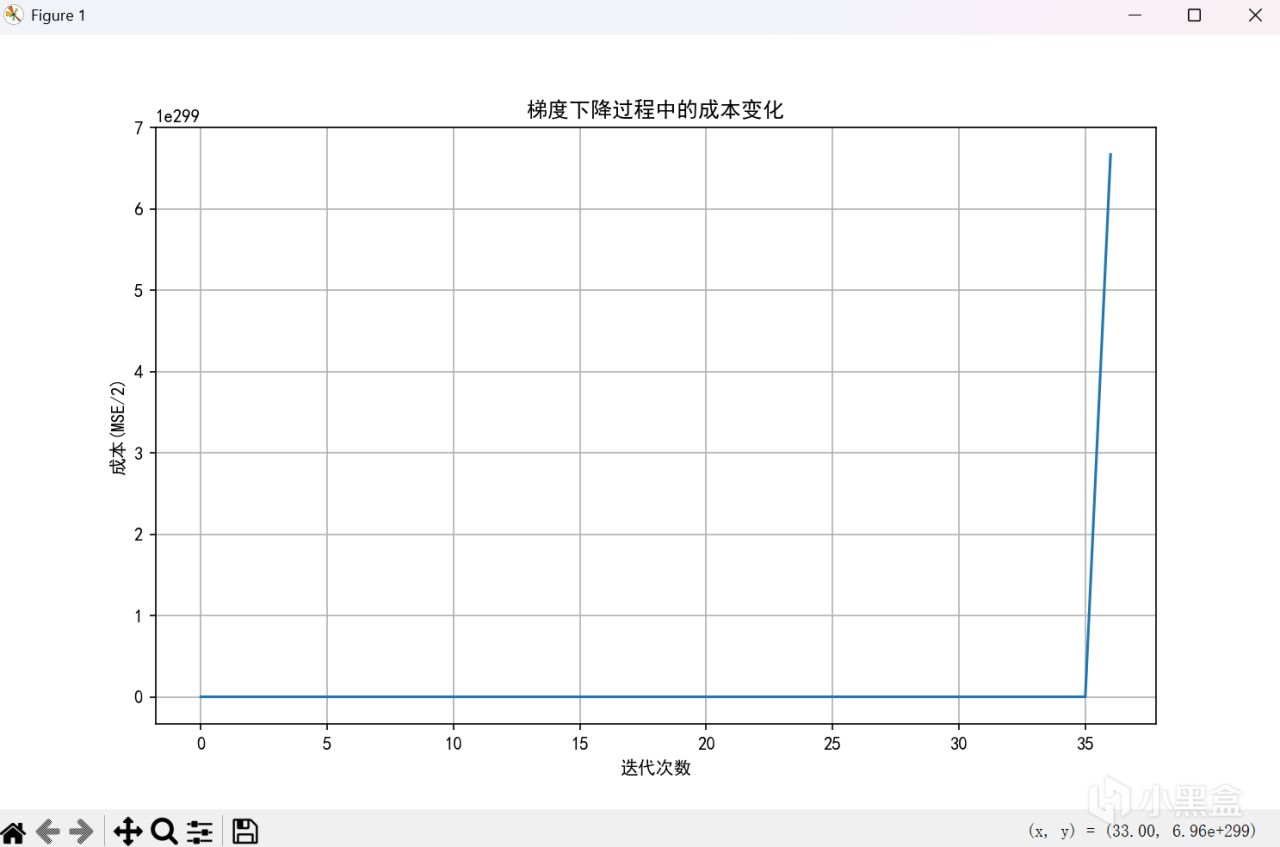
alpha = 0.00001
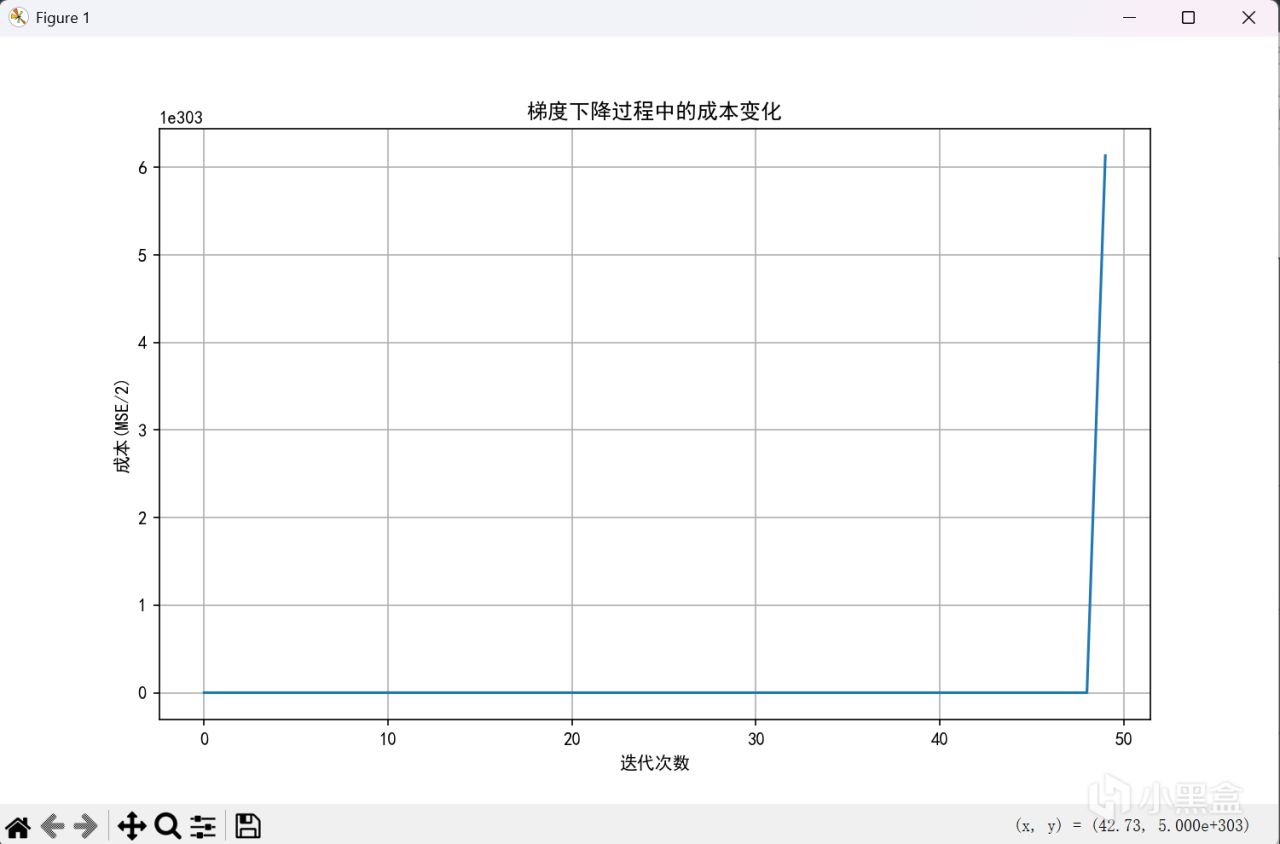
alpha = 0.000001
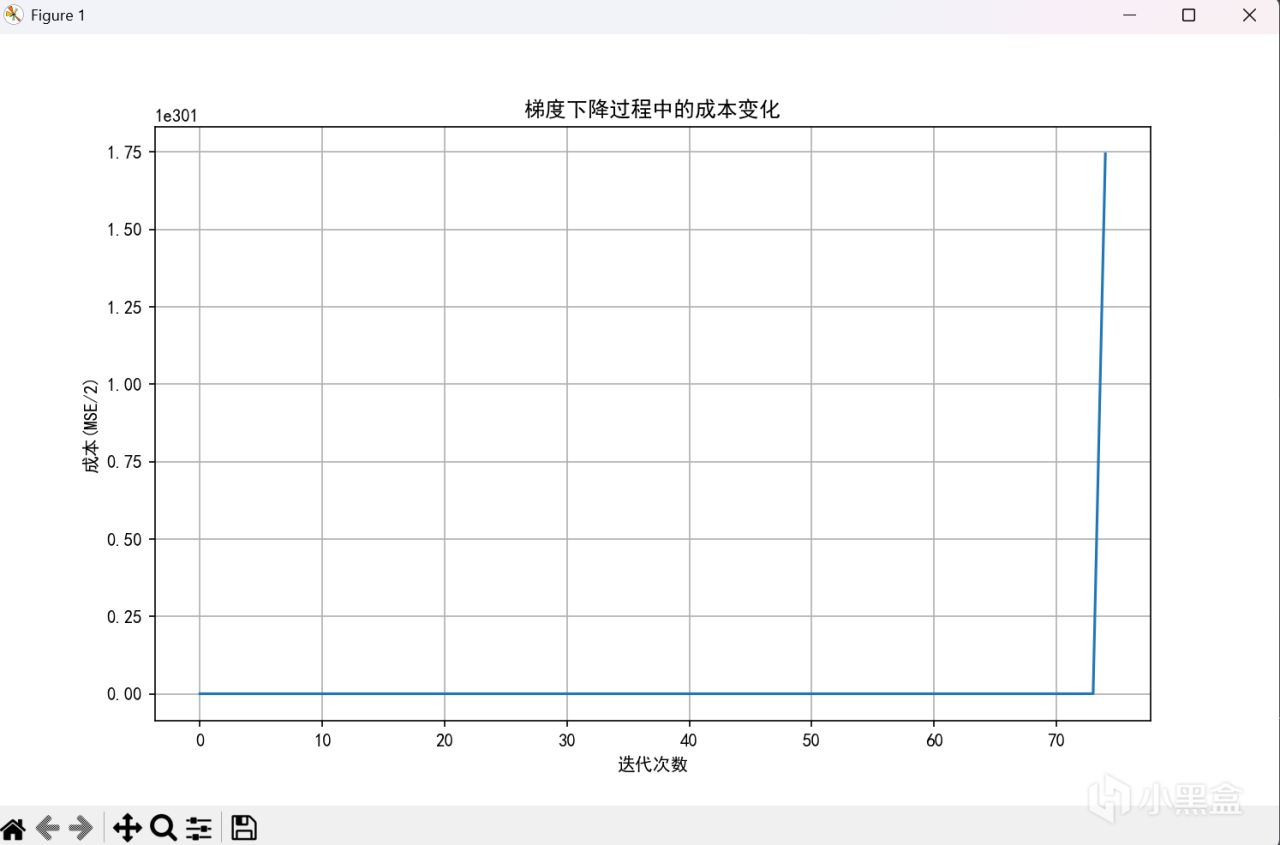
alpha = 0.00000001
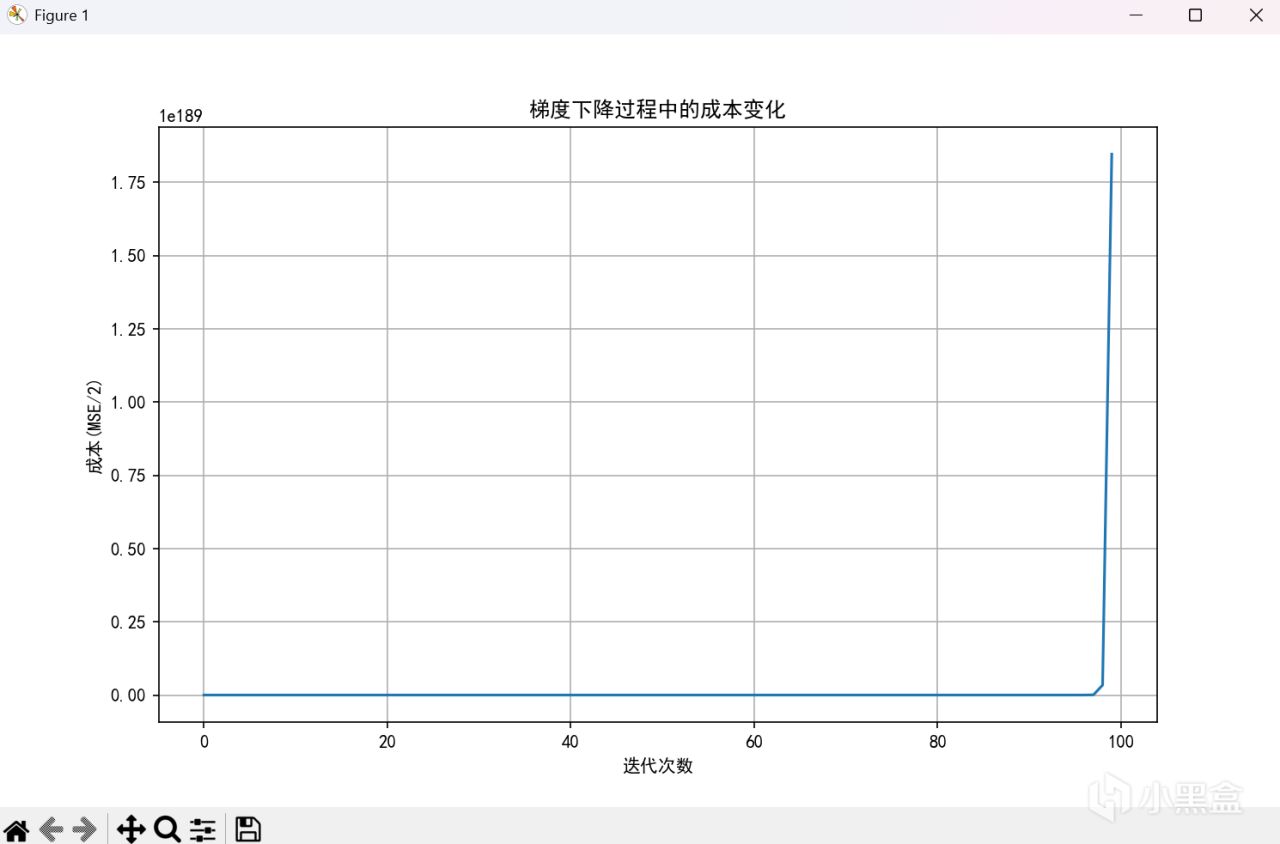
alpha = 0.00000001
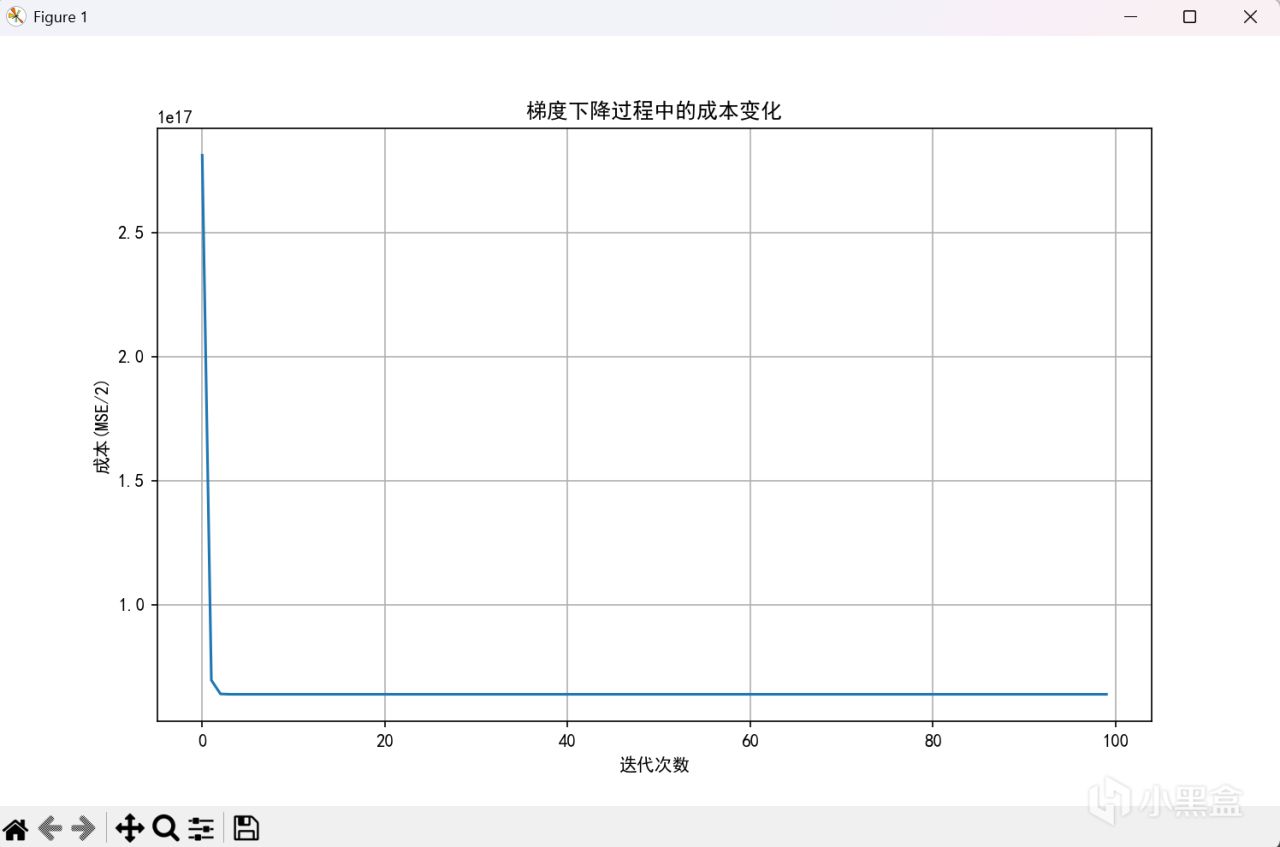
alpha = 0.000000001
666,菸斗不演了,可以看到,當學習率到十的負九次方纔能正常工作。但是不用擔心,歸一化來嘍。
先用最大值歸一化舉例子

最大值歸一化
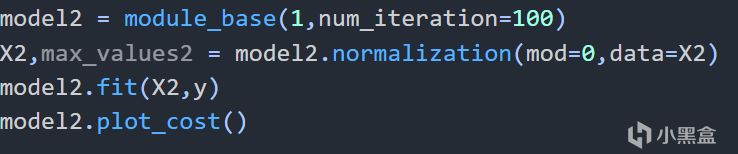
歸一化後構建模型,alpha爲1
看看結果吧!
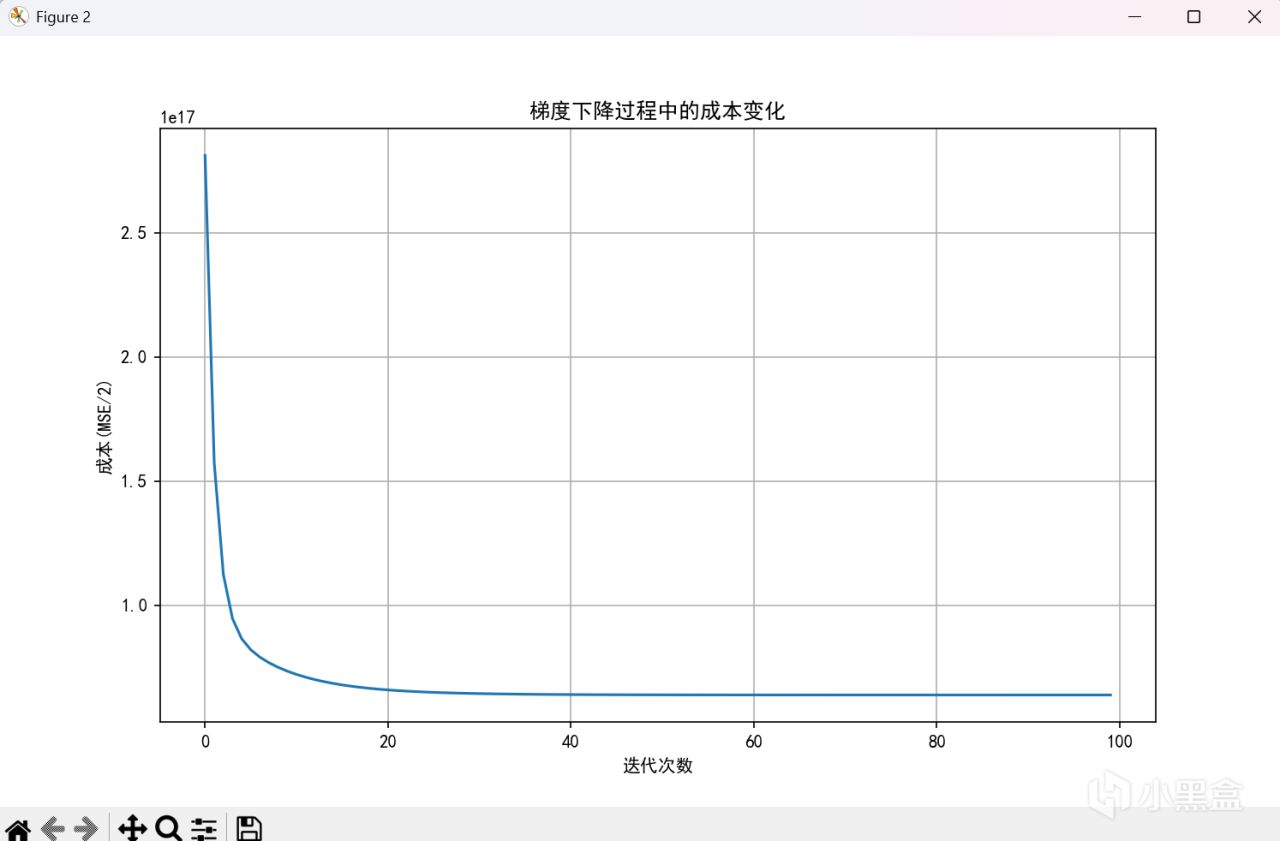
歸一化後,損失函數(alpha爲1)
可以看到學習率高到爲1時,一樣能正常工作,顯然這種能非常方便更改alpha來調試模型的方法非常好。除此之外,我們還可以使用很多其他方法,這裏舉例幾種

Min-Max縮放
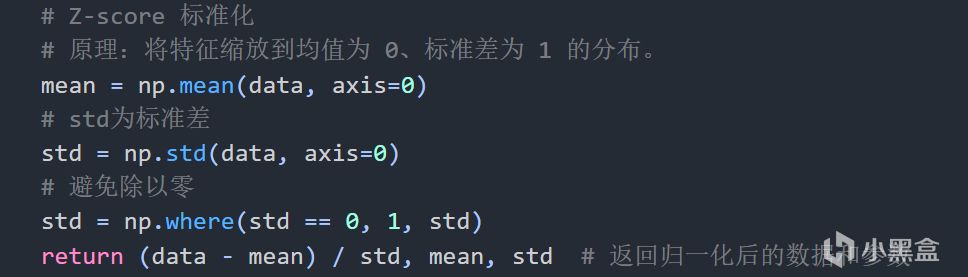
Z-score 標準化
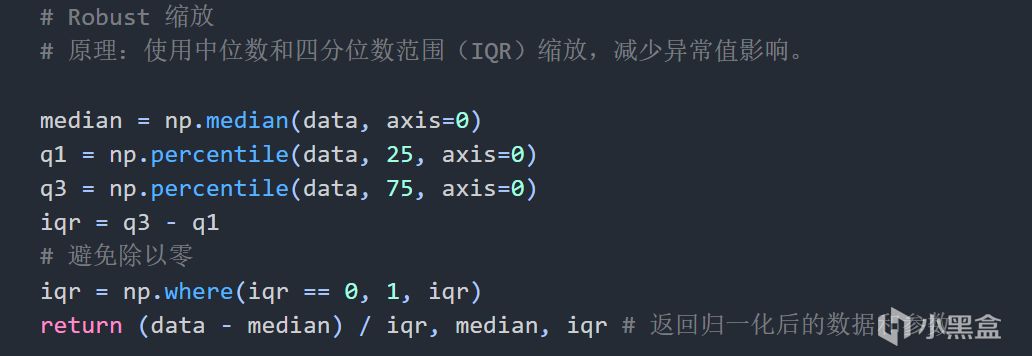
Robust 縮放
學習率基本都在0.1~1左右,這裏不展示具體代碼,結果如下
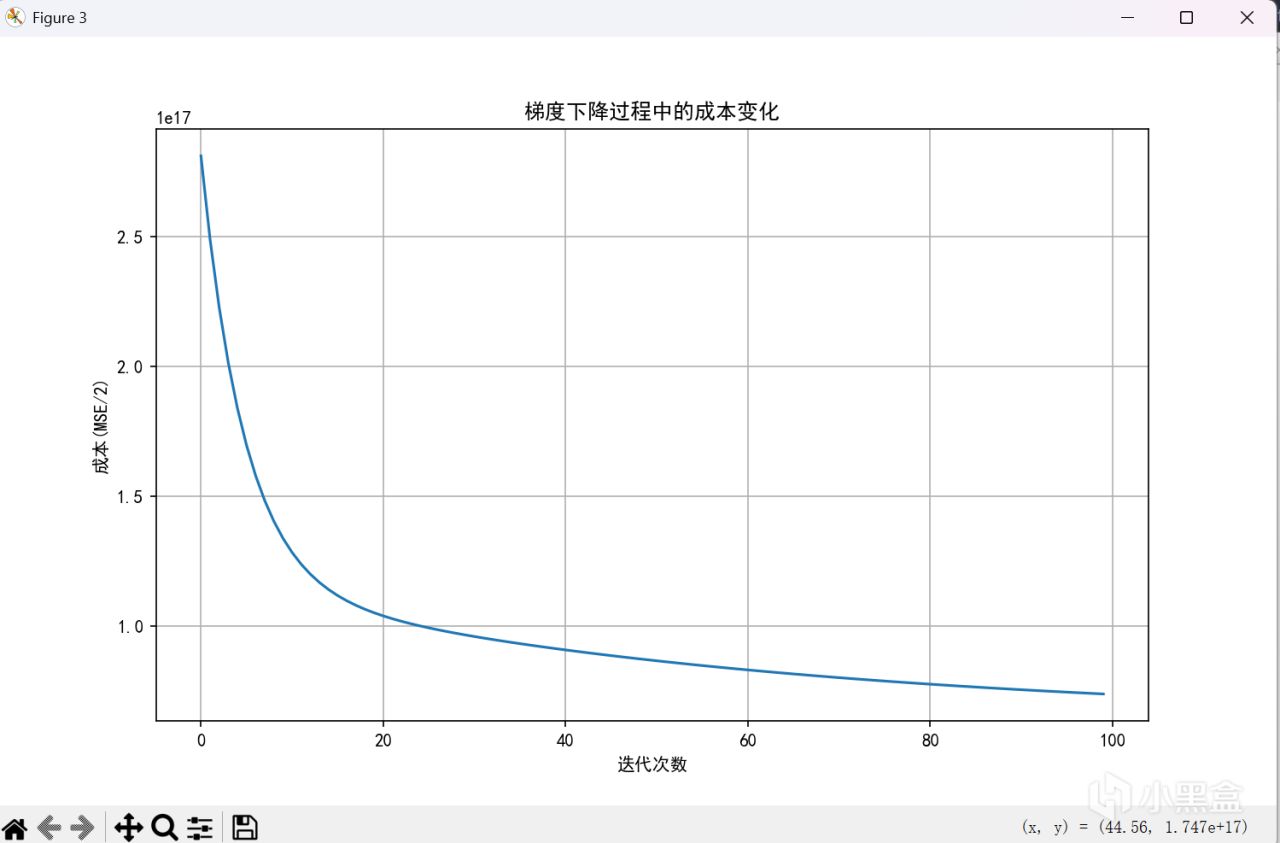
Min-Max縮放
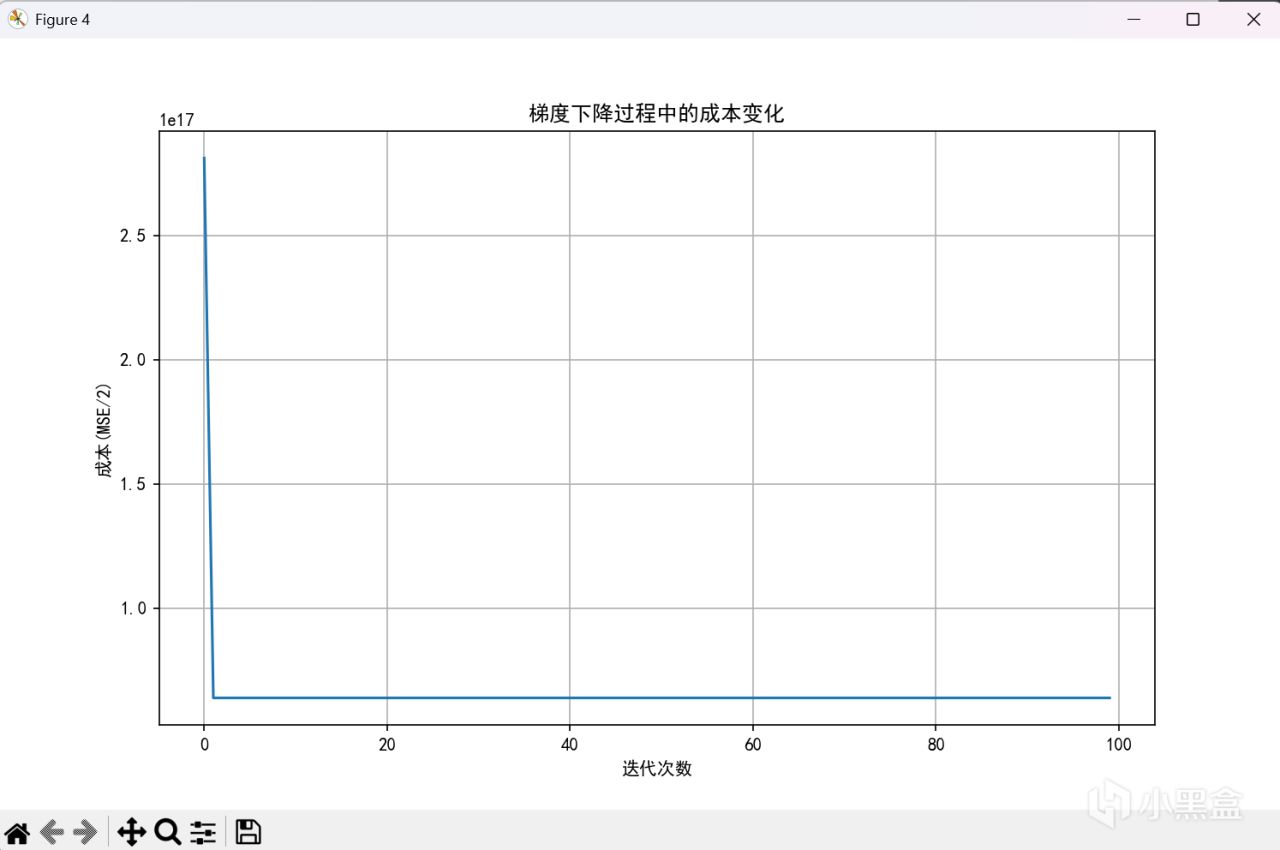
Z-score 標準化
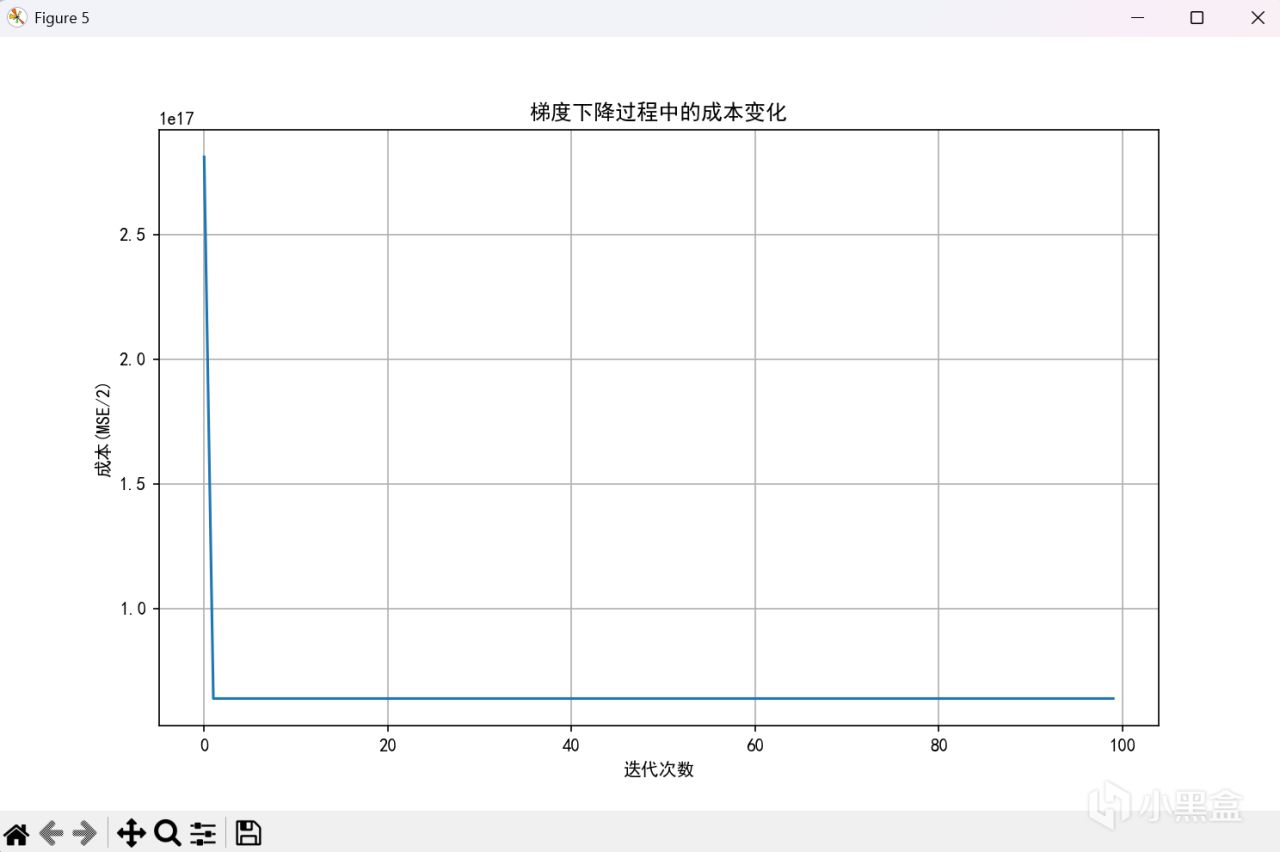
Robust 縮放
可以看到不同的歸一化方法有不同的結果,對於不同的數據分佈,總會有更適合的方法,所以沒有什麼方法好壞之分,只有適合與否。但無一例外,在這種歸一化的方法下,我們能更好的處理更復雜數據的情形,構建模型時,更好的把握學習率的範圍,便於調試
常用初次使用範圍
最大值歸一化:0.01 到 0.1
均值歸一化:0.001 到 0.01
Z-score 標準化:0.0001 到 0.01
L1/L2 歸一化:0.1 到 1
Robust 縮放:0.00001 到 0.001
在之後,我們可以逐步擴大alpha值,一般是倍數增加,例如三倍,四倍,然後觀察是否模型擬合更好,更快。
除了速度與便於調試,在尋找極小值時,歸一化也可以在一定程度上很好的避免陷入局部最小值,如之前未歸一化,很可能出現一些局部最小值,而因爲alpha值小,讓數據數值小的特徵值陷入在局部最小值中,從而失去最優解。我們可以對上訴模型都進行一萬次迭代,觀看結果
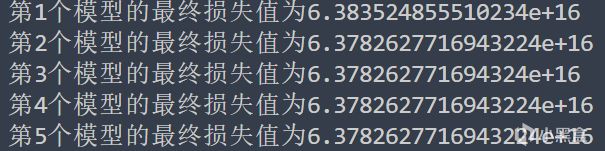
輸出
可以看到,第一個(未進行歸一化)明顯損失值大的多),而其他模型迭代後基本上損失值相同,說明都到達了真正的最小值點附近,而第一個有可能跳入了局部最小值,或者有可能是速度太小了,還需要更多的迭代,無論是哪一種,都足以證明歸一化的優勢所在!
所以在機器學習中,歸一化基本上成爲了不可或缺的操作。
具體內容就這些了,歡迎hmy討論分享,要是覺得鼠鼠寫的對自己有幫助或者感興趣,麻煩點點贊和轉發,讓更多人看到,謝謝大家。
如果你是初次看到,想要看更多內容,不妨點個關注,後續不定期更新。
上個帖子疑似被限流了,剛發帖一個小時就1000瀏覽量,到現在才漲了50不到的瀏覽量,嗚嗚,其實無所謂了,能幫助到有需要的人,也是鼠鼠的榮幸了呀
更多遊戲資訊請關註:電玩幫遊戲資訊專區
電玩幫圖文攻略 www.vgover.com















