今天我們來講一下c++中的遞歸算法
原理/理論
遞歸是編程中一種強大的技術,它允許函數自我調用。在C++中,遞歸通常用於解決某些類型的問題,如分治算法等。下面我們將深入探討C++中的遞歸知識,包括其原理、用法、作用等。
遞歸的原理
遞歸的核心思想是將問題分解爲更小的子問題。這些子問題通常與原始問題相似,但規模更小。通過解決這些子問題,我們可以組合它們的解決方案來獲得原始問題的解決方案。
遞歸的基本步驟如下:
基線條件:這是遞歸終止的條件。當問題規模足夠小時,基線條件將被滿足,遞歸調用將停止。
遞歸步驟:這是將問題分解爲更小子問題的步驟。函數會自我調用,每個子問題的規模都比原始問題小。
組合子問題的解決方案:當所有的子問題都被解決後,它們的解決方案被組合起來以形成原始問題的解決方案。
遞歸的作用
遞歸在編程中有很多用途,包括:
解決問題:許多問題可以通過遞歸有效地解決,特別是那些可以自然分解爲更小子問題的問題。例如,排序算法(如快速排序和歸併排序)、搜索算法(如深度優先搜索和廣度優先搜索)以及圖算法(如Dijkstra算法和Prim算法)都可以用遞歸來實現。
簡化代碼:對於某些問題,使用遞歸來編寫代碼可以使代碼更簡潔、更易於理解。由於每個遞歸調用都做類似的事情,這也有助於代碼複用。
抽象和分治策略:遞歸是一種強大的抽象工具,可以用來解決複雜的問題。通過將問題分解爲更小的子問題,我們可以更容易地理解和解決原始問題。此外,分治策略(即將問題分解爲獨立的子問題,然後解決這些子問題並將結果組合起來)也是遞歸的核心概念。
理解複雜概念:對於初學者來說,遞歸可能是一個難以理解的概念。然而,一旦掌握了它,就可以更好地理解許多複雜的編程概念,如動態規劃、堆棧、隊列等。
處理無限數據結構:雖然在實際編程中很少遇到無限數據結構,但理論上,遞歸是處理這類數據結構的唯一方法。例如,無限斐波那契數列和無限鏈表只能通過遞歸來處理。
遞歸函數
遞歸函數是一種特殊的函數,它在其定義或實現中直接或間接地調用自身。遞歸函數通常用於解決一些可以通過分解爲更小的子問題來解決的問題。在C++中,遞歸函數的定義和實現與其他函數類似,但是需要在函數的主體中調用自身。
遞歸函數的基本結構如下:
基線條件:這是遞歸終止的條件。當問題規模足夠小時,基線條件將被滿足,遞歸調用將停止。
遞歸步驟:這是將問題分解爲更小子問題的步驟。函數會自我調用,每個子問題的規模都比原始問題小。
組合子問題的解決方案:當所有的子問題都被解決後,它們的解決方案被組合起來以形成原始問題的解決方案。
生動的理解
遞歸,就是在運行的過程中調用自己本身
A. 構成遞歸需具備的條件:
子問題須與原始問題爲同樣的事,且更爲簡單:
這是遞歸的核心概念。一個函數要成爲遞歸的,它必須在其定義中調用自身來處理比原始問題更小的子問題。這些子問題必須與原始問題相似,但規模更小。這樣,通過解決這些子問題,我們可以組合它們的解決方案來得到原始問題的解決方案。不能無限制的調用本身,必須有個出口,化簡爲非遞歸狀況處理:
爲了避免無限遞歸,遞歸函數必須有一個或多個基線條件。當滿足基線條件時,遞歸調用停止。基線條件是遞歸終止的條件,通常當問題規模足夠小時滿足。這樣,遞歸函數最終會化簡爲非遞歸狀況處理,從而避免無限遞歸。
B. 遞歸可以解決的問題:
階乘:階乘是一個典型的遞歸問題。例如,計算5的階乘(5!)可以分解爲計算4的階乘(4!)和加上5。然後,4的階乘可以分解爲計算3的階乘(3!)和加上4,依此類推,直到基線條件1! = 1。
斐波那契數列:這是一個著名的遞歸問題。每個斐波那契數都是前兩個數的和。例如,要計算第n個斐波那契數,可以遞歸地計算第n-1個和第n-2個斐波那契數,然後將它們相加。
漢諾塔:這是一個經典的遞歸問題。漢諾塔問題要求將一堆盤子從一個柱子移動到另一個柱子,每次只能移動一個盤子,並且不能將一個較大的盤子放在較小的盤子上面。這個問題的解決方案是一個典型的遞歸過程,其中將問題分解爲更小的子問題(移動較小的盤子)並將其解決,然後將結果組合起來(移動較大的盤子)以解決原始問題。
楊輝三角的存取:楊輝三角是一個經典的數學問題,可以通過遞歸的方式求解。例如,可以使用遞歸來計算楊輝三角中的第n行數字。
字符串迴文判斷:這是一個可以通過遞歸解決的問題。可以使用遞歸來比較字符串的首尾字符,然後遞歸地比較字符串的中間部分,直到字符串的長度爲1或0。
字符串全排列:全排列可以通過遞歸的方式求解。可以使用遞歸來生成所有可能的排列,直到所有字符都被排列。
二分查找:二分查找是一個經典的遞歸算法。它通過將搜索空間一分爲二來找到目標值。在每次遞歸調用中,算法將搜索空間縮小一半,直到找到目標值或搜索空間爲空。
樹的深度求解:樹的深度可以通過遞歸的方式求解。對於每個節點,算法將其子節點的最大深度作爲該節點的深度。在每個遞歸調用中,算法處理一個子樹並返回該子樹的深度,直到達到葉節點或沒有子節點爲止。
C. 遞歸的過程:
遞歸過程通常包含以下幾個步驟:
定義:定義函數的基本結構並明確函數的名稱和輸入參數。
基線條件:確定函數的基線條件。這是遞歸終止的條件,通常當問題規模足夠小時滿足。
遞歸步驟:將問題分解爲更小的子問題,並調用自身來處理這些子問題。這個步驟是遞歸的核心部分,它使函數能夠自我調用以解決更小的子問題。
組合子問題的解:當所有的子問題都被解決後,將這些子問題的解組合起來以形成原始問題的解。這個步驟是將遞歸轉化爲非遞歸的過程,通過組合子問題的解來獲得原始問題的解。
返回值:在函數體中返回結果或執行其他必要的操作以完成函數的執行。
通過以上步驟,遞歸函數實現了將複雜問題分解爲更小的子問題並最終解決原始問題的目的。然而,使用遞歸時需要注意防止無限遞歸和棧溢出等問題,確保在基線條件下及時終止遞歸調用。
部分代碼,思路來自csdn
舉幾個例子
階乘
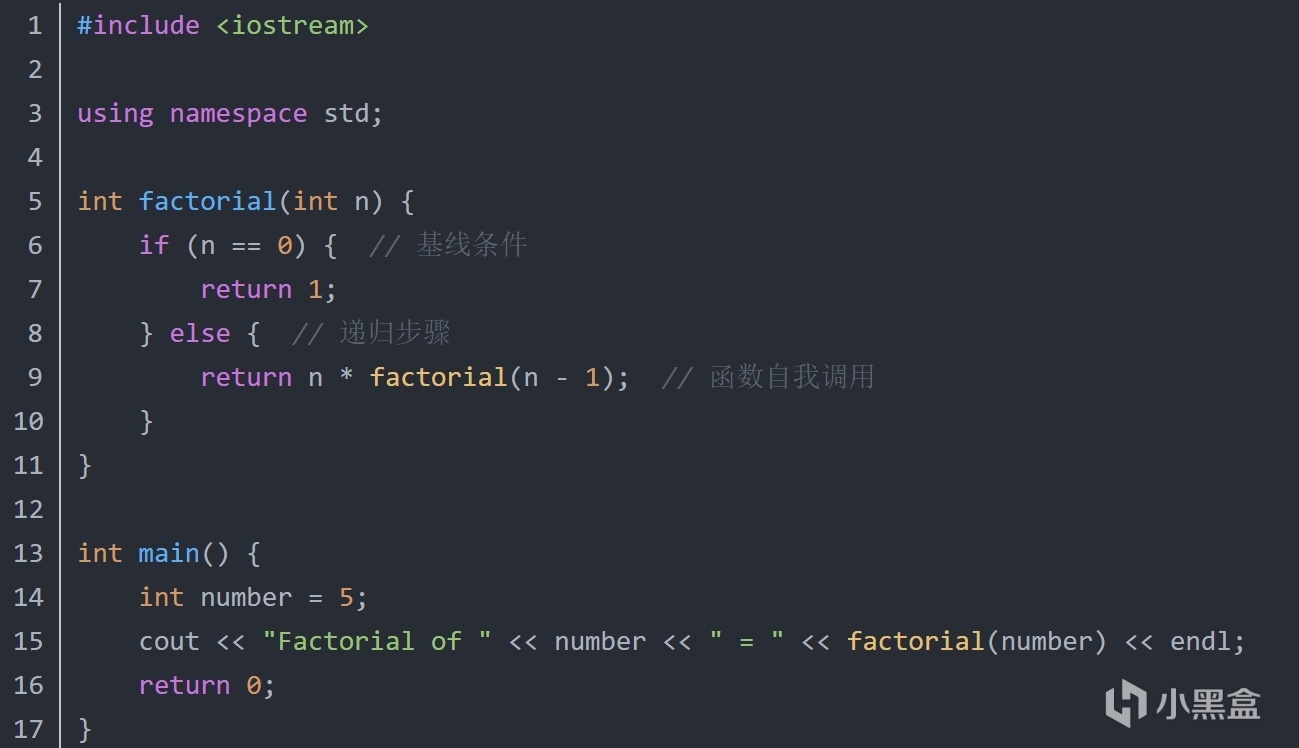
斐波那契數列
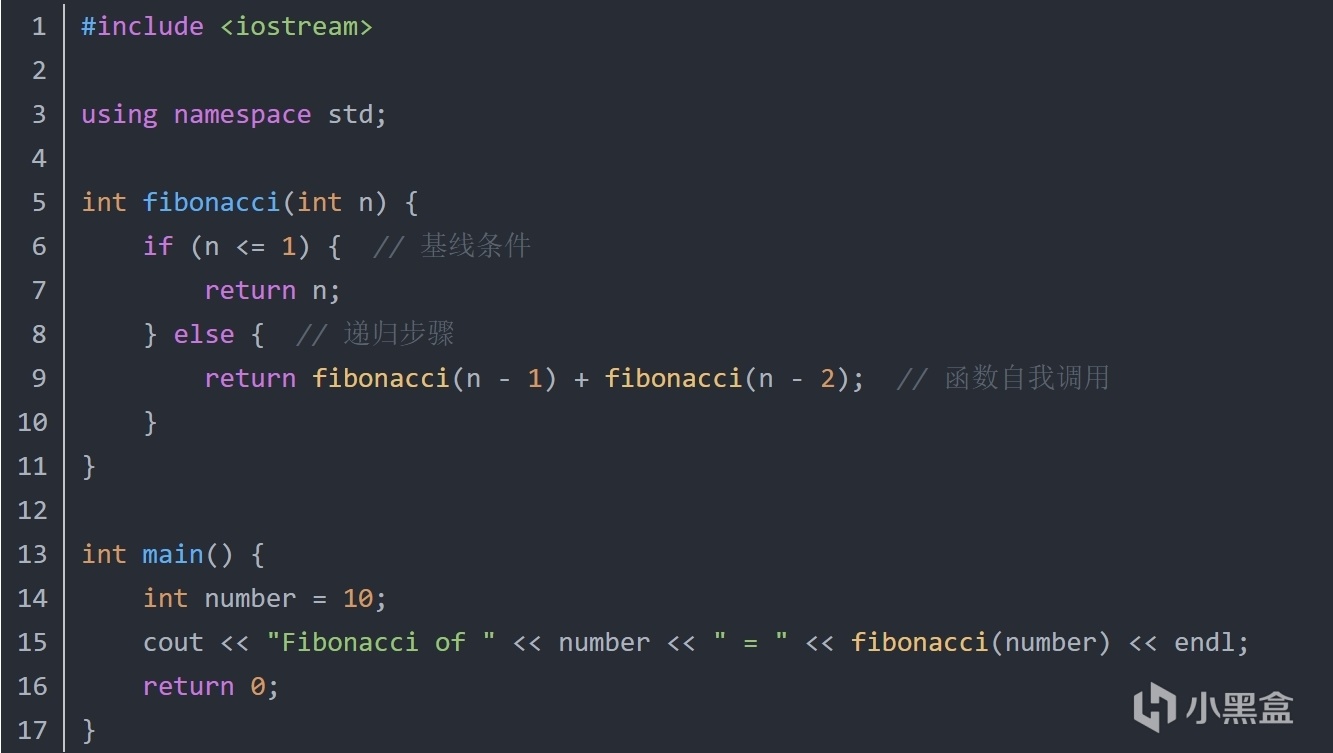
字符串迴文判斷
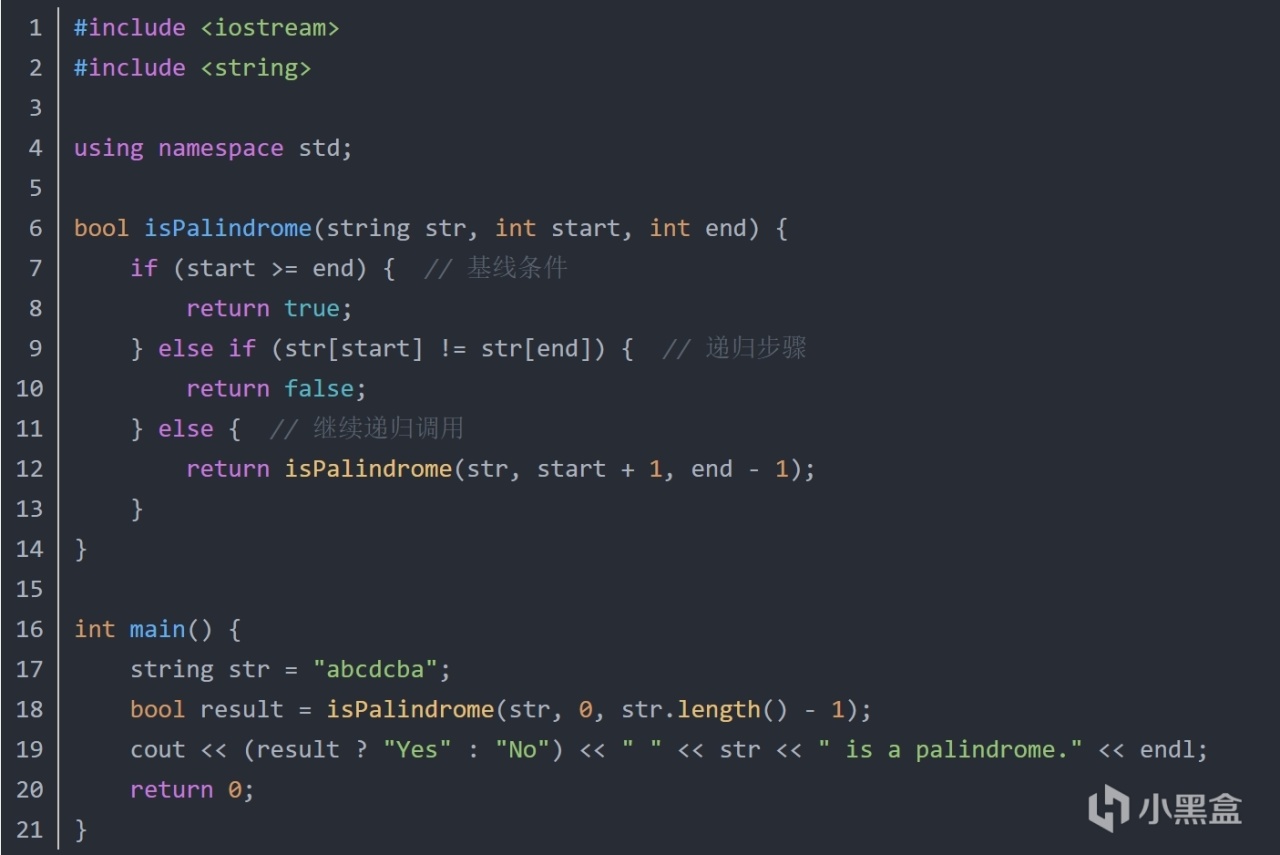
看到這裏,你已經基本瞭解了c++中的遞歸算法
下面是一個遞歸的習題練習一下:
由鍵盤錄入一個正整數,求該整數中每個數字出現的次數。
輸入:19931003
輸出:
0 2
1 2
3 2
9 2
更多遊戲資訊請關註:電玩幫遊戲資訊專區
電玩幫圖文攻略 www.vgover.com


















