《Cypher》第四章 維吉尼亞密碼的破譯原理及代碼實現

Github倉庫鏈接：https://github.com/ZzySlhbcf/Cypher-Decoder

一、從凱撒密碼說起

1.1 簡單介紹凱撒密碼

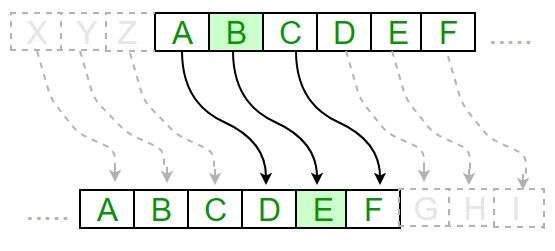
Caesar密碼是最早的單表代換密碼，也是一種簡單的位移密碼。其基本思想爲：通過把字母在字母表上向左（或向右）按照一個固定的位數進行偏移來實現加密和解密。

明文序列：Cypher

密文序列：EARJGT（明文右移2位）

用數學公式進行描述（右移）：Dn(x)=(x+n) mod 26，其中x爲字母在字母表中的序號（A=0，B=1...Z=25），n爲偏移量。

1.2 頻率分析法

Caesar密碼爲單表位移加密，就是簡單的將字母表整體偏移。也就是說26個不同的明文字母在偏移後對應的密文字母也是不同的，可以輕鬆得到密文字母的頻率與其對應的明文字母頻率是相同的（不存在不同明文對應相同密文來改變頻率）。

假設"E"對應的密文爲"A"，如果在明文中"E"爲12%，密文中的"A"也爲12%。

字母頻率是指各個字母在文本中出現的頻率，常被應用於密碼學，尤其是可破解古典密碼的頻率分析。根據統計，在英語材料中最常出現的字母是e，大約佔12~13%，出現最少的字母是z，不到0.1%。

移位密碼、仿射密碼和單表代換密碼都沒有破壞統計規律，所以我們可以直接根據字母的頻率分析進行破解。

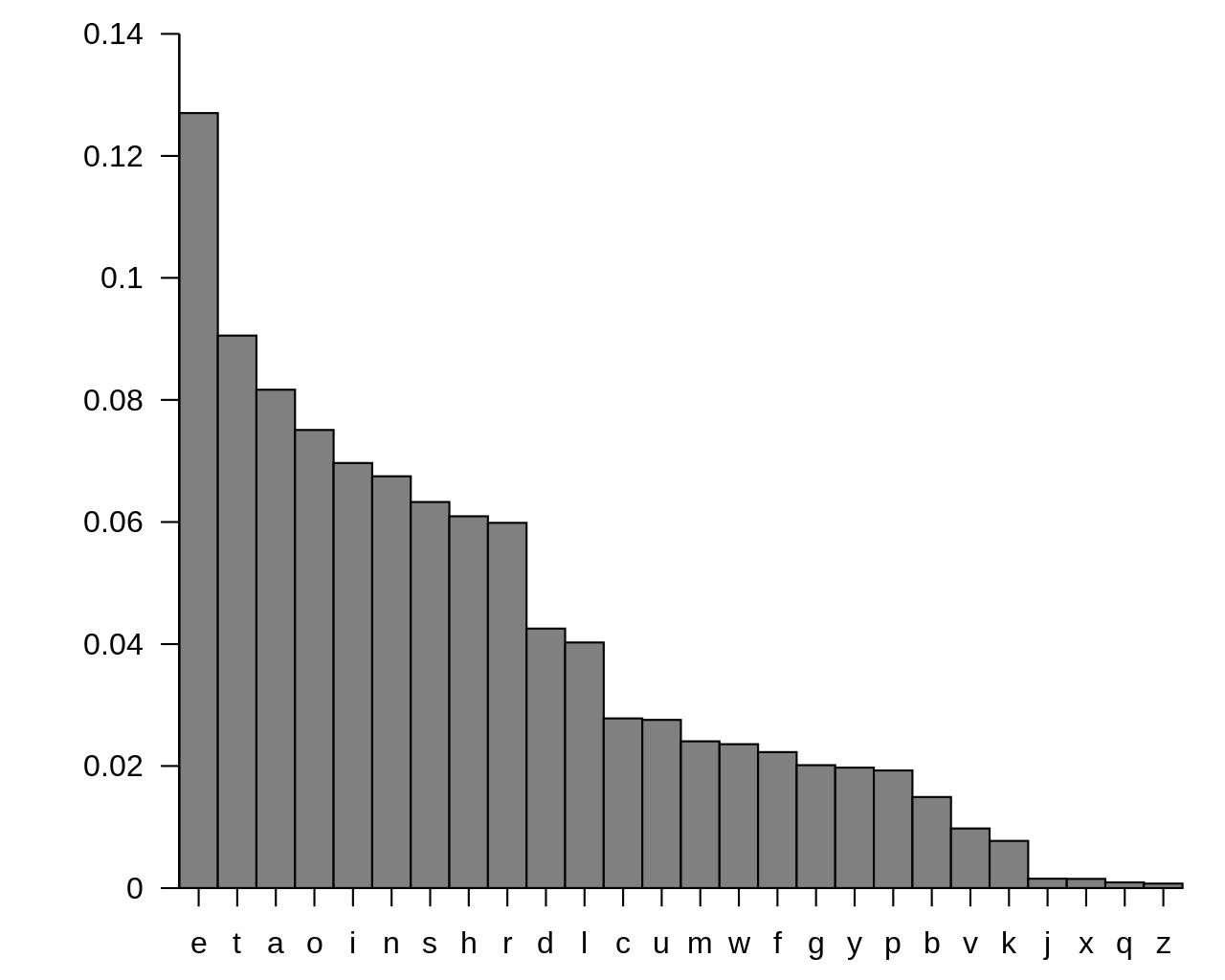
如果在密文中，如果"T"出現的次數最多，那麼它很大概率對應"E"。

1.3 頻率分析法的弊端

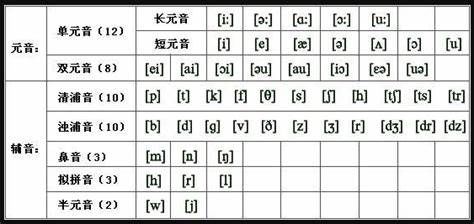
頻率分析法是基於統計的，也就說如果樣本過小，概率將會不準確。這時我們可以通過文章的結構或者語法來分析，英文中出現頻率最高的單詞是：the, of, and, a, to, in……如果在密文中出現最多次的字母組合很可能就是其中的一個，另外我們還可以通過分析輔元音在單個單詞中的組合與佔比來分析密文結構。

如上的所有分析都是基於一個條件的：密文沒有破壞明文的字母頻率，但是如果密文破壞了字母頻率，例如不同明文字母替換爲相同的密文字母或相同明文字母替換爲不同密文字母，那麼對於密文本身的頻率分析將變得沒有意義，這也就是多表代換密碼一開始難以破解的原因之一。

二、維吉尼亞密碼

2.1 維吉尼亞密碼的加密原理

Vigenere密碼是一種簡單的多表代換密碼，即由多個偏移量不同的凱撒密碼構成。這些偏移量組成了密鑰，如密鑰"ACBZ"對應的偏移量組就是(1,3,2,26)。

注意："1 3 2 26"是根據遊戲中的對照表（如下圖所示），現實中"ACBZ"對應的應該是"0 2 1 25"，即"A-Z"對應"0-25"。本文是遊戲中的內容爲依據來編寫代碼，如需更正可自行修改。

現在假設我們的密鑰爲"cypher"，即偏移量組爲(3,25,16,8,5,18)，而我們現在需要加密"i like playing games"。

1. 將密文中的空格刪去，根據密鑰長度從前往後進行進行分組[(ilikep)，(laying)，(games)]。

2. 每一組中的明文字母根據密鑰對應位置的偏移量向右進行偏移，如第一組中的第2個字母"L"，對應偏移量爲25得到密文，即En=(12+25) mod 26=K。

3. 對每一組進行如上操作得到密文爲[(LKYSJH)，(OZOQSB)，(JZCJK)]。

這樣我們就得到了密文"L KYSJ HOZOQSB JZCJK"。解密與加密步驟相同，偏移與加密相反即可，如加密是向右偏移，解密則向左偏移。

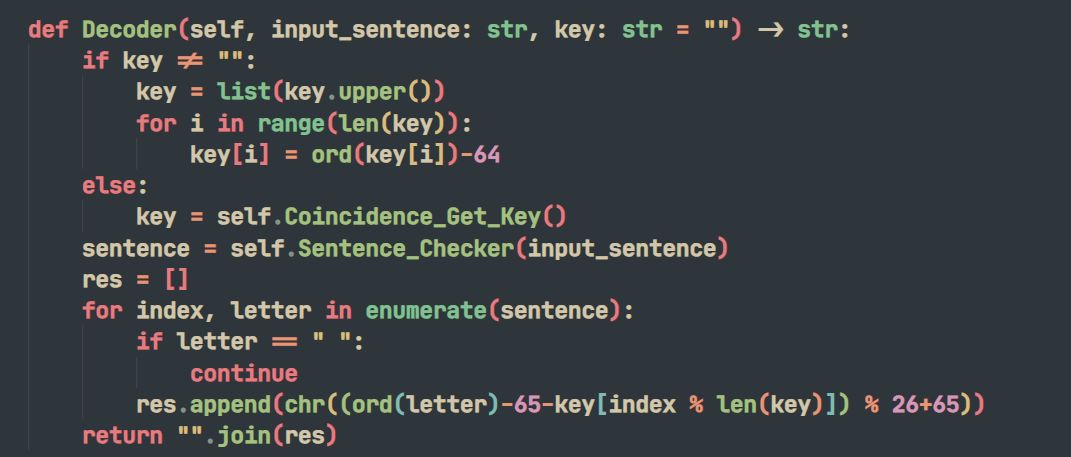
假設明文爲E，密文爲D，密鑰爲K，明文序列下標爲i，則

D(i)=[E(i) + K(i mod len(K))] mod 26

E(i)=[D(i) - K(i mod len(K))] mod 26

2.2 維吉尼亞密碼破譯原理

在上一小節的示例"i like playing games"中可以看到，其中兩個"i"被分別加密成了"L、Y"兩個密文，而"l、y"被同時加密爲"O"。這也就是說維吉尼亞密碼會改變字母頻率，字母頻率分析法就沒有作用了，即我們無法通過分析明文和密文結構來解密。

我們可以從密鑰尋找突破點。每一組明文段都用相同的密鑰，不難發現如果正好有三個相同字母組被分割到了不同組內的相同位置，那麼他們的密文就是相同的。例如[(athe)，(abcd)，(bthe)]，選取任意一個長度爲4的密鑰，明文中的"the"按照上一節的步驟都會被加密成同一個密文。

由此我們可以確定解密的三個步驟：

1. 確定密鑰的長度

2. 確定密鑰的內容

3. 根據密鑰恢復明文

三、確定密鑰的長度

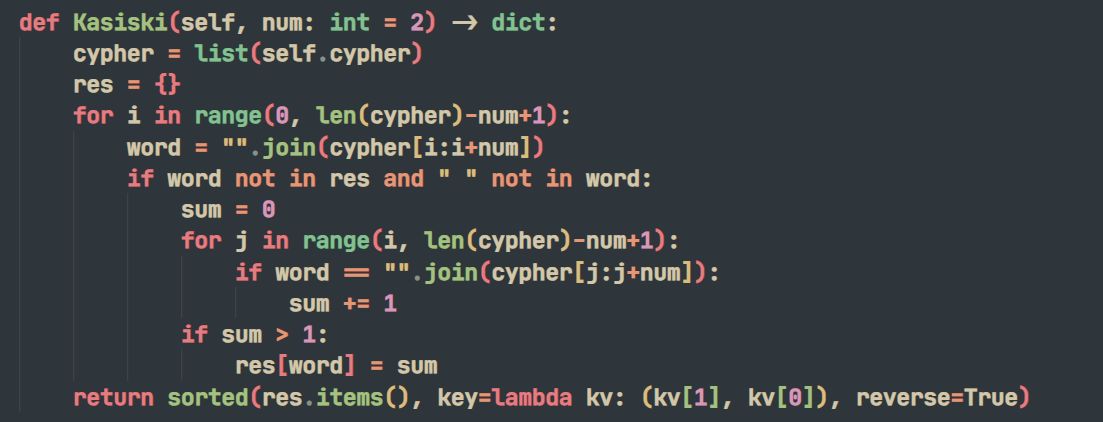
3.1 Kasiski測試

按照如上思路，分別獲取兩個相同密文段的首字母的下標，按照例子就是1和9。我們只要找到首字母的下標之差（9-1=8）中大於相同密文段長度（3）的最大公因數GCD即可，8的最大公約數爲4，正好可以與密鑰長度4對應上。

這種方法雖然簡單但是是有漏洞的，不同的密文段有可能對應相同的明文段（密鑰長度過長）。而且，如果找不到足夠多的重複字母組，那麼Kasiski測試也等於無用。想要這種方法奏效，就需要密鑰長度適中。

3.2 重合指數法（Coincidence Index）

在一個正常語義的英文文本中，和一個無意義亂序的英文文本中，字母出現次數的統計特徵是有明顯差異的，可以利用這種差異來幫助我們自動化的破解密碼。回到1.2中的字母頻率圖，拿其中頻率最高的"e"舉例子，字母e在英文文本中出現的概率約爲12.68%。易得我們在文本內任選兩個字母都是"e"的概率爲12.68%^2。類似的，對於任一概率爲P(i)的字母 i，隨機選取兩個字母后都是 i 的概率爲P(i)^2。在一串無規律的字母中，我們隨意抽取兩個字母，由於每個字母被抽到的概率相同，因此抽取的兩個字母相同的概率爲26*（1/26）^2=0.0385。

這裏我們定義重合指數CI，即某個密文中隨機無放回地抽取其中的兩位，這兩位的字母相同的概率。

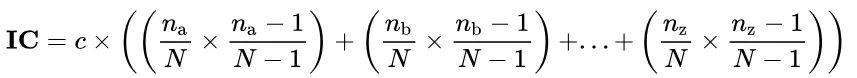
其中c是歸一化係數，用於對不同字母表進行歸一化處理（英語爲26），n下標a是字母“a”出現在文本中的次數，N是文本的長度。重合指數也可以用求和的形式來表示：

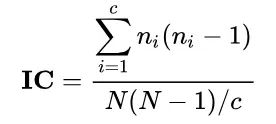
一個明文足夠長的平移密碼的重合指數接近0.0687，而一段完全隨機的文本中，重合指數更接近0.038。由此可以判斷密碼爲單表代換還是多表代換，維吉尼亞密碼並不是簡單的單表平移密碼，它是由明文每個位置的字母按照對應的偏移得來的。也就說只要把密文拆解開，按照下標 i mod m（密鑰長度） 分組重新組合爲m個密文序列，這些序列CI的平均值應該是接近自然語言的重合指數的。

假設密鑰長度只有2，明文的奇數位是同一偏移量，偶數位也爲同一偏移量。

接下來我們只需要測試出哪個m可以使密文均值CI接近0.0687即可，這個很大概率爲密鑰長度，可以用3.1的Kasiski測試進行測試。

四、確定密鑰內容

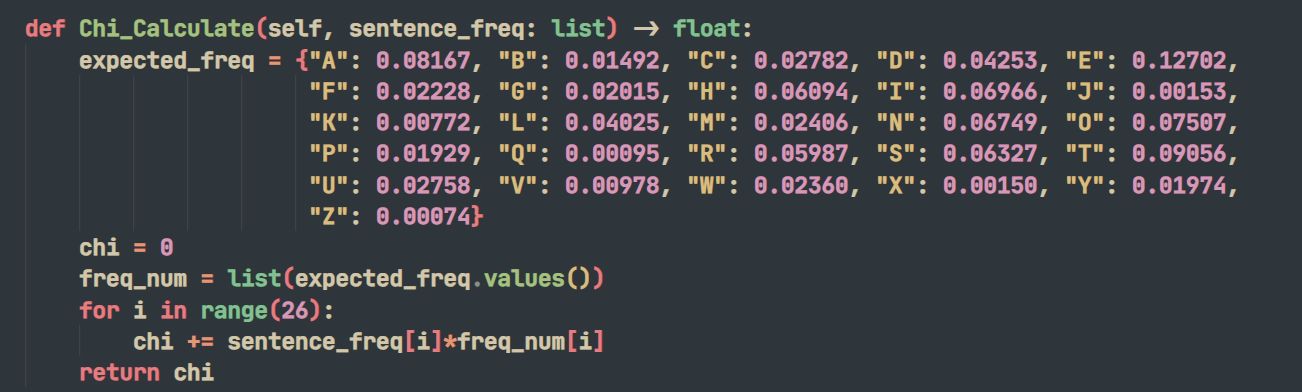
4.1 Chi測試

在得到密鑰長度m後，將密文按照下標 i mod m重新組合爲m個密文序列。每組對應的明文只有26中可能性（每組的偏移量相等）。暴力窮舉的範圍從26^L一下子降到了26^m，雖然下降了很多，但是這個數字依舊很大。字頻統計也不能用——因爲每組內的密文都是間隔 m−1 個字母取到的，這就意味者每組的樣本量很小，用組內的字頻會導致結果失真。

再將目光放回1.2中的字母頻率圖，對於每一組密文，都有26種位移可能，其中正確的偏移會使其IC指數接近0.065。但是有一個問題，由於樣本數量小，IC一樣不準確。IC指數定義中兩次抓取都是再密文中進行的，我們略微做出改變，一次抓取再密文段中，另一次抓取正常英語文本中，這樣就可以緩解密文段樣本數量小的問題。

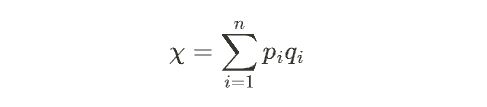
這樣計算出來的稱爲“擬重合指數”，就是 SUM(P(i)Q(i)) ，其中P(i)就是密文的某一種位移後得到的字母的頻率，Q(i))就是字母的在自然語言中一般概率，也就是上面的26字母頻率表。這個“擬重合指數”越大，說明兩段文本的字母的分佈律越相像，也就代表密文段越像自然語言。

經過如此操作，我們將窮舉次數再一次減少到了26*m次，以這種方法普通人花些時間也可以成功解密。

4.2 擬重合指數法的步驟

1. 統計每組密文中每個字母的頻數 f(0) 、 f(1)…f(25) 。

2. 計算每組密文的長度L，計算26個字母在該組中的頻率分佈 p(0) 、 p(1)…p(25) 。

3. 對序列p(i)進行偏移，得到26種排序。當位偏移量爲 k 的時候，原本的排序就會變爲 p(26−k) 、 p(27−k)…p(25) 、p(0) 、 p(1)…p(25−k) ，可將這種排序設爲26維向量組。

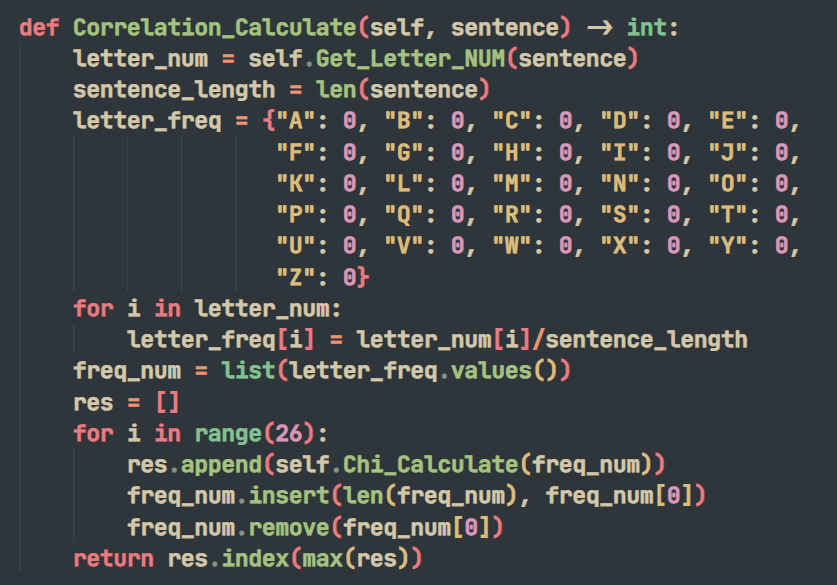
4. 將26×L的向量組與1×26的自然語言字母概率進行卷積 Correlation(Pk,Q)=SUM[p((k+1) MOD 26)q(i)]，其中最大的值所對應的爲該組密文的偏移量。

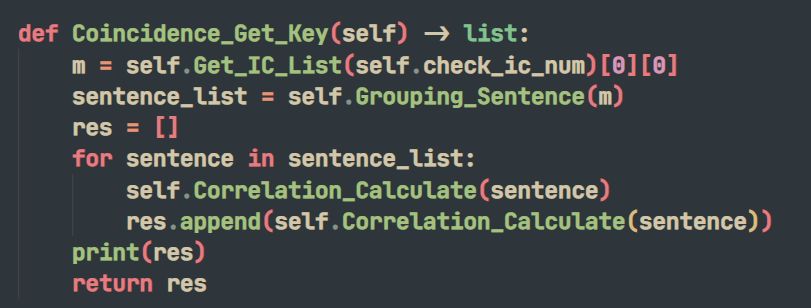
五、小試牛刀

密文序列：

"LAFLUIWOYWPADUFHSNBVSWVNDZQDUFRBPLUYQPLWLPHZRLUEDUBSYMIPRDIJHTYQUCUZYLKFRSKHZBUHULUEKPQFOYLYSSAMWOCWHZOLGDTDDPPOFDDTGOPYUDGWOYOSDRYKVVDVLAULRZYGWPLJZYQKYPTWVLJIAFHHSWOMUVDDAPLMJLUEPVLRNPDWFXWMQAFHZSEQCFAGQDFLJFLHLDSWCLMQLFXUBULBDUBVPVWFQHWYUHRHJGSOCUZZXAGFVLILQVAFDARKPQLZCQAGULJBUCZAMPL"

首先重合指數法得到最大的IC值所對應的密鑰長度m=3

根據密鑰長度對密文進行分組。

對每組密文段求其擬重合指數，並將其最大的擬重合指數所對應的偏移量記爲該組的偏移量。

對每組進行如上操作後得到密鑰列表，最後根據密鑰解密即可。

明文：

I think that I can help  you to pass an hour in an interesting and profitable manner," said Holmes, drawing his chair up to the table. "I am fairly familiar with all forms of secret writings, and am myself the author of a trifling monograph upon the subject, in which I analyze one hundred and sixty separate ciphers. But I confess that this is entirely new to me.

六、結語

如果密鑰是完全隨機、與明文的長度一致且只使用過一次，維吉尼亞密碼理論上是不可破譯的。然而，這種情況下密鑰本身而非密文便成了關鍵，這被稱爲一次性密碼本。

最後以下圖最左邊的小故事結束本篇文章。

BEALE（比爾密碼）
1885年的弗吉尼亞州，旅店店主Robert Moriss出版了一個小冊子，裏面講述了他的一位客人讓他保管的一些重要文件，但是那位客人再也沒有回來取走它們的故事。這些文件包含了1份註釋和3份密文，據說包含了被掩埋的黃金藏匿處的方位。第二份密文是以《獨立宣言》作爲密鑰，已被破譯，而其他兩份至今仍未被破譯。