【新智元導讀】英偉達首席科學家揭祕英偉達 GPU 能如此成功的 4 個主要原因,4 個關鍵數據帶來持續的行業競爭力。

如今的英偉達,穩坐 GPU 霸主王座。
ChatGPT 誕生後,帶來生成式 AI 大爆發,徹底掀起了全球的算力爭奪戰。
前段時間,一篇文章揭露,全球對 H100 總需求量超 43 萬張,而且這樣的趨勢至少持續到 2024 年底。

過去的 10 年裏,英偉達成功地將自家芯片在 AI 任務上的性能提升了千倍。
對於一個剛剛邁入萬億美元的公司來說,是如何取得成功的?
近日,英偉達首席科學家 Bill Dally 在硅谷舉行的 IEEE 2023 年熱門芯片研討會上,發表了關於高性能微處理器的主題演講。
在他演講 PPT 中的一頁,總結了英偉達迄今爲止取得成功的 4 個要素。
摩爾定律在英偉達的「神奇魔法」中只佔很小的一部分,而全新「數字表示」佔據很大一部分。
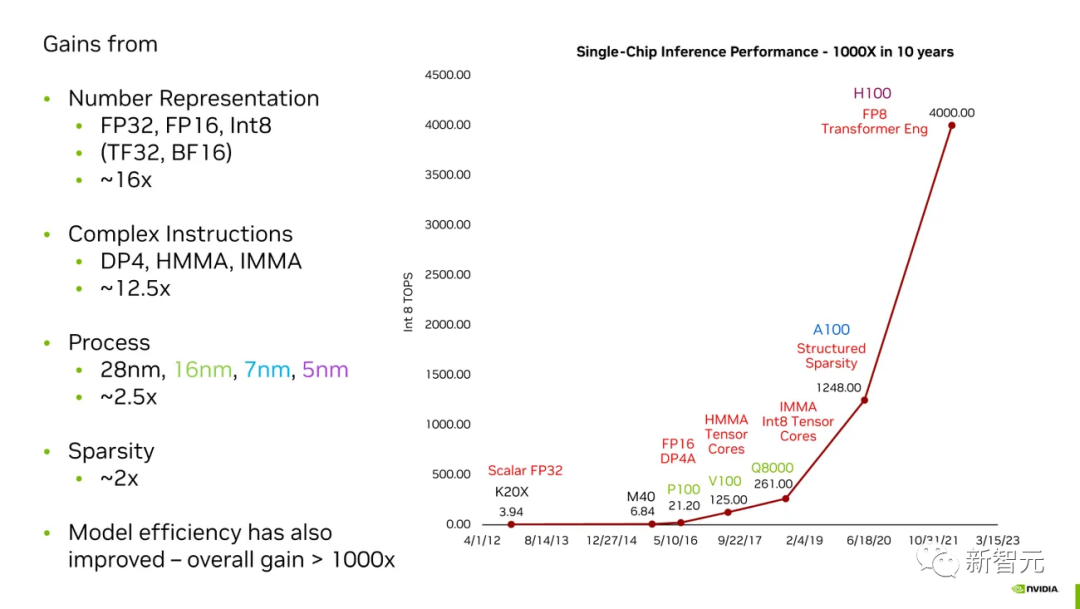
英偉達如何在 10 年內將其 GPU 在 AI 任務上的性能提高了千倍
把以上所有這些加在一起,你就會得到「黃氏定律」(Huang's Law)。
黃教主曾表示,「由於圖形處理器的出現,摩爾定律已經站不住腳了,代之以一個新的超強定律。」

數字表示:16 倍提升
Dally 表示,總的來說,我們最大的收穫是來自更好的「數字表示」。
這些數字,代表着神經網絡的「關鍵參數」。
其中一個參數是權重,模型中神經元與神經元之間的連接強度。
另一個是激活度,神經元的加權輸入之和乘以多少才能決定它是否激活,從而將信息傳播到下一層。
在 P100 之前,英偉達 GPU 使用單精度浮點數來表示這些權重。
根據 IEEE 754 標準定義,這些數字長度爲 32 位,其中 23 位表示分數,8 位基本上是分數的指數,還有 1 位表示數字的符號。
但機器學習研究人員很快發現,在許多計算中,可以使用不太精確的數字,而神經網絡仍然會給出同樣精確的答案。
這樣做的明顯優勢是,如果機器學習的關鍵計算 —— 乘法和累加 —— 需要處理更少的比特,可以使邏輯變得更快、更小、更高效。
因此,在 P100 中,英偉達使用了半精度 FP16。
谷歌甚至提出了自己的版本,稱作 bfloat16。
兩者的區別在於分數位和指數位的相對數量:分數位提供精度,指數位提供範圍。Bfloat16 的範圍位數與 FP32 相同,因此在兩種格式之間來回切換更容易。

回到現在,英偉達領先的圖形處理器 H100,可以使用 8 位數完成大規模 Transformer 神經網絡的某些任務,如 ChatGPT 和其他大型語言模型。
然而,英偉達卻發現這不是一個萬能的解決方案。
例如,英偉達的 Hopper 圖形處理器架構實際上使用兩種不同的 FP8 格式進行計算,一種精度稍高,另一種範圍稍大。英偉達的特殊優勢在於知道何時使用哪種格式。

Dally 和他的團隊有各種各樣有趣的想法,可以從更少的比特中榨取更多的人工智能性能。顯然,浮點系統顯然並不理想。
一個主要問題是,無論數字有多大或多小,浮點精度都非常一致。
但是神經網絡的參數不使用大數,而是主要集聚在 0 附近。因此,英偉達的 R&D 重點是尋找有效的方法來表示數字,以便它們在 0 附近更準確。
複雜指令:12.5 倍
「提取和解碼指令的開銷遠遠超過執行簡單算術操作的開銷,」 Dally 說道。
他以一個乘法指令爲例,執行這個指令的固定開銷達到了執行數學運算本身所需的 1.5 焦耳的 20 倍。通過將 GPU 設計爲在單個指令中執行大規模計算,而不是一系列的多個指令,英偉達有效地降低了單個計算的開銷,取得了巨大的收益。
Dally 表示,雖然仍然存在一些開銷,但在複雜指令的情況下,這些開銷會分攤到更多的數學運算中。例如,複雜指令整數矩陣乘積累加(IMMA)的開銷僅佔數學計算能量成本的 16%。
摩爾定律:2.5 倍
保持摩爾定律的有效性需要數十億美元的投資、非常複雜的工程上的設計,甚至還會帶來國際關係的不穩定。但這些投入都不是造成英偉達 GPU 的成功的主要原因。
英偉達一直在使用全球最先進的製造技術來生產 GPU——H100 採用臺積電的的 N5(5 納米)工藝製造。這家芯片工廠直到 2022 年底纔開始建設它的其下一代 N3 工藝。在建好之前,N5 就是業內最頂尖的製造工藝。
稀疏性:2 倍
將這些網絡變得「稀疏」以減少計算負荷是一項棘手的工作。
但是在 A100,H100 的前身中,英偉達引入了他們的新技術:「結構化稀疏性」。這種硬件設計可以強制實現每四個可能的剪枝事件中的兩次,從而帶來了一種新的更小的矩陣計算。
Dally 表示:「我們在稀疏性方面的工作尚未結束。我們需要再對激活函數進行加工,並且權重中也可以有更大的稀疏性。」=
來源:IT之家
更多遊戲資訊請關註:電玩幫遊戲資訊專區
電玩幫圖文攻略 www.vgover.com


















