一文講清所有掃雷定式

好久不見！在此前的文章中，我們學習了掃雷中最重要的三大工具：11連通器原理、減法公式和降階思維。，下面我們先快速回顧一下它們的核心要點（如果想要深入瞭解請看此前的文章）：

• 11連通器原理：當棋盤上出現兩個相鄰的數字“1”時，如果其中一邊靠近某個“1”的一整列格子沒有雷，那麼相對的另一邊對應列也必然沒有雷；反之，如果一邊必然有雷，則另一邊也必然有雷。

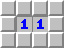
該效果可無限連通：

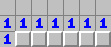
• 減法公式：當兩個數字相鄰，且一個比另一個大（如“1”和“3”），若大數字一側的未開格子數正好等於兩個數字的差值（例如 3-1=2 個格子），那麼這幾個格子全是雷，而小數字一側的格子則全都安全。

• 降階思維：如果某些格子已經百分之百確定爲雷，我們就可以“假裝”它們不存在，並把它們周圍數字的數值都減 1。這樣得到的新局面與原局面是完全等價的，可以讓複雜問題轉化爲更簡單的問題。

上下兩者等價

掃雷定式本質上是這三者的組合，例如

這兩者的左下角一定不是雷，因爲這是11連通器+降階思維，兩者都等價於11連通器，而右側無雷，則左側也一定無雷

掌握了這些工具後，你會發現：在實戰中，不僅要會用邏輯，還需要熟悉一些“定式”。所謂定式，就是某個數字周圍所有可能的雷分佈模式。

接下來，我們會按照以下順序展開介紹：

1. 單數字定式：從1開始到4，展示它們最常見的雷分佈模式。看起來最簡單，但是最實用，因爲其本質上是圖形記憶，通過這些定式，我們不再需要在棋盤上反覆數數，而是能通過快速識別圖形來判斷：這個數字周圍的雷是否已經全部確定。

2. 多數字定式：當多個數字組合在一起時，周圍雷的分佈會更復雜。我們將從涉及數字大小較小、格子較少的情況出發，逐漸遞進到更復雜的組合

   1. 升階與降階：在多數字定式中，我們會不斷使用“降階思維”，把複雜局面化簡爲已經熟悉的單數字或低階定式

單數字定式

從 5 開始，單數字定式的本質就變成了“陰刻”和“陽刻”的區別：

• 5 的定式可以看作是 3 的定式的補集

• 6 的定式是 2 的定式的補集

• 7 的定式是 1 的定式的補集

• 8 則意味着周圍所有格子全是雷

看下面兩張圖你就懂了：

由於 5、6、7、8 這些數字在實戰中出現得相對較少，而且它們的模式都能由低數字的補集推導出來，所以只要熟練掌握 1、2、3、4 的單數字定式，就已經完全足夠應對大多數情況

另外，單數字定式中還有一個非常重要的繼承原理：當某個雷型不僅滿足了當前數字的要求，還能讓新打開的相鄰格子繼續滿足它們的數字條件時，這個雷型就能被“繼承”下去，從而推動局面自動展開

繼承有時候不一定要把對應的雷找出來，例如下面的11挖坑定式

11挖坑定式

如果通過11連通器開出了一個1，那麼就可以繼續往下挖（因爲坑頂的1把雷限制在了二個坑邊格子中，只是二選一）

如果中間又挖出了一個1，還可以繼續往下挖一層

把屏幕翻轉90度，你就會發現這就是豎着的11連通器

同理還有斜切32續開定式 本質是11連通器+降價思維

以下兩種也可以續開

該定式在實戰中較爲常見，快速識別的技巧是擁有一個“同時影響3和2的雷”

11隔牆定式（比較少見）

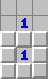
12減法公式 最常見的減法公式

同理有13、14、23、24、25……的情況，將在下面演示

22靠牆定式

本質上是12減法公式+降價思維

121定式 本質上是對稱的兩個12減法公式

121定式如果挖出了2，也可以觸發繼承

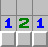
升階可得232單頂定式：

1221定式、12221定式、122221定式 本質上都是12減法公式的複合

單翹邊122定式

單翹邊1222定式

212定式、翹邊212定式

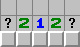
本質上是減法公式的12情況，所以兩邊的雷可以有多種可能

其它排列組合就不展示了

雙翹邊222定式

頂角121不定式

這其實是不定式，但實戰中經常遇到，爲防止大家瞎猜放在這裏

內角121定式

斜角121定式

這個很容易出現繼承

缺角121定式

這個也很容易出現繼承

13定式

如果左邊是牆還會出現這種情況（所有和1有關的減法公式比如12、14都會這樣）

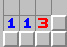
如果13的後面出現了2，還會出現13背2定式

13背2定式可以通過降階思維變爲14背2/3、24背2、25背2/3定式等各種形態，例如：

313定式 本質是對稱的13減法公式 下方開出3可繼承

132定式 本質依然是13減法公式+繼承

翹邊32定式 很簡單但很常見，實戰需快速反應

232定式 中間的3可以有無數個，只要兩邊是2就成立

熟知上面的所有定式，就足以你馳騁掃雷戰場，雖然還有大量的定式沒有展示，但是正如前面所說，所有的定式本質上都是11連通器、減法公式和降階思維的排列組合，例如

看起來很複雜，但上面的降階後是121定式，而121定式又是兩個12減法公式；下面的降階後是11連通器

所以比死背定式更重要的，是在實戰中積累肌肉記憶，快去試試吧~

感謝各位的觀看，下一篇教學，我們將討論“什麼時候應該標雷，什麼時候不應該標雷”，若大家有興趣，可以關注我獲取最新信息哦~